题目内容
已知二次函数f(x)=x2+2(p-2)x+p,若在区间[0,1]内至少存在一个实根c,使f(c)>0,则实根p的取值范围是
- A.(1,4)
- B.(1,+∞)
- C.(0,+∞)
- D.(0,1)
C
分析:由于二次函数f(x)=x2+2(p-2)x+p的图象是开口方向朝上的抛物线,故二次函数f(x)=x2+2(p-2)x+p在区间[0,1]内至少存在一个实数c,使f(c)>0的否定为对于区间[0,1]内的任意一个x都有f(x)≤0,即f(0),f(1)均小于等0,由此可以构造一个关于p的不等式组,解不等式组即可求出实数p的取值范围.
解答:二次函数f(x)在区间[0,1]内至少存在一个实数c,使f(c)>0的否定是:
对于区间[-1,1]内的任意一个x都有f(x)≤0,
∴
即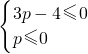
解得p≤0,
∴二次函数在区间[0,1]内至少存在一个实数c,
使f(c)>0的实数p的取值范围是 (0,+∞)
故选C.
点评:本题考查的知识点是一元二次方程的根的分布与系数的关系,其中根据二次函数的图象是开口方向朝上的抛物线,得到对于区间[0,1]内的任意一个x都有f(x)≤0时, 是解答本题的关键.
是解答本题的关键.
分析:由于二次函数f(x)=x2+2(p-2)x+p的图象是开口方向朝上的抛物线,故二次函数f(x)=x2+2(p-2)x+p在区间[0,1]内至少存在一个实数c,使f(c)>0的否定为对于区间[0,1]内的任意一个x都有f(x)≤0,即f(0),f(1)均小于等0,由此可以构造一个关于p的不等式组,解不等式组即可求出实数p的取值范围.
解答:二次函数f(x)在区间[0,1]内至少存在一个实数c,使f(c)>0的否定是:
对于区间[-1,1]内的任意一个x都有f(x)≤0,
∴

即
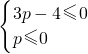
解得p≤0,
∴二次函数在区间[0,1]内至少存在一个实数c,
使f(c)>0的实数p的取值范围是 (0,+∞)
故选C.
点评:本题考查的知识点是一元二次方程的根的分布与系数的关系,其中根据二次函数的图象是开口方向朝上的抛物线,得到对于区间[0,1]内的任意一个x都有f(x)≤0时,
 是解答本题的关键.
是解答本题的关键. 
练习册系列答案
相关题目