题目内容
 如图,设由抛物线C:x2=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S(阴影部分).
如图,设由抛物线C:x2=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S(阴影部分).(1)设直线l与抛物线C交于两点A(x1,y1),B(x2,y2),且x1<x2,直线l的斜率为k,试用k表示x2-x1;
(2)求S的最小值.
【答案】分析:(1)由抛物线C的方程可得焦点的坐标,设A(x1,y1),B(x2,y2),进而可设直线l的方程,与抛物线联立消去y,根据韦达定理求得x1+x2和x1x2的值,进而根据 求得x2-x1.
求得x2-x1.
(2)根据 化简整理得
化简整理得 ,令
,令 ,进而根据t的范围求得S的范围,得到最小值.
,进而根据t的范围求得S的范围,得到最小值.
解答:解:(1)可得点F(0,1),
设直线l的方程为y=kx+1直线l与抛物线C交于两点A(x1,y1),B(x2,y2),
由 ,得x2-4k-4=0,
,得x2-4k-4=0,
∴x1+x2=4k,x1x2=-4,又x1<x2,
∴ .
.
(2)所求的面积:
=
=
=
=
令 ,则t≥1,有k2=t2-1,
,则t≥1,有k2=t2-1,
S= =
=

在[1,+∞)上为单调递增函数,∴当t=1,即k=0时,S有最小值 .
.
点评:本题主要考查了抛物线的应用及抛物线与直线的关系.常需要把直线方程和抛物线方程联立,根据韦达定理解决问题.
 求得x2-x1.
求得x2-x1.(2)根据
 化简整理得
化简整理得 ,令
,令 ,进而根据t的范围求得S的范围,得到最小值.
,进而根据t的范围求得S的范围,得到最小值.解答:解:(1)可得点F(0,1),
设直线l的方程为y=kx+1直线l与抛物线C交于两点A(x1,y1),B(x2,y2),
由
 ,得x2-4k-4=0,
,得x2-4k-4=0,∴x1+x2=4k,x1x2=-4,又x1<x2,
∴
 .
.(2)所求的面积:

=

=

=

=

令
 ,则t≥1,有k2=t2-1,
,则t≥1,有k2=t2-1,S=
 =
=

在[1,+∞)上为单调递增函数,∴当t=1,即k=0时,S有最小值
 .
.点评:本题主要考查了抛物线的应用及抛物线与直线的关系.常需要把直线方程和抛物线方程联立,根据韦达定理解决问题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
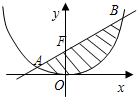 如图,设由抛物线C:x2=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S(阴影部分).
如图,设由抛物线C:x2=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S(阴影部分). (2007•揭阳二模)如图,线段AB过y轴负半轴上一点M(0,a),A、B两点到y轴距离的差为2k.
(2007•揭阳二模)如图,线段AB过y轴负半轴上一点M(0,a),A、B两点到y轴距离的差为2k. (2013•杭州模拟)如图,由半圆x2+y2=1(y≤0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,且曲线C经过点(2,3).
(2013•杭州模拟)如图,由半圆x2+y2=1(y≤0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,且曲线C经过点(2,3). 如图,设由抛物线C:x2=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S(阴影部分).
如图,设由抛物线C:x2=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S(阴影部分).