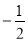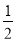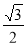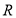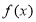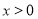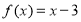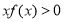题目内容
已知函数 (其中
(其中 ),满足
),满足 .
.
(Ⅰ)求函数 的最小正周期
的最小正周期 及
及 的值;
的值;
(Ⅱ)当 时,求函数
时,求函数 的最小值,并且求使函数取得最小值的
的最小值,并且求使函数取得最小值的 的值.
的值.
(1)
 ;(2)最小值为
;(2)最小值为 ,此时
,此时
【解析】
试题分析:(1)由 求函数的最小正周期,然后根据
求函数的最小正周期,然后根据 与
与 ,确定
,确定 的取值;(2)由题中所给的
的取值;(2)由题中所给的 的范围,求出整体
的范围,求出整体 的范围,再结合
的范围,再结合 的图像,不难求得
的图像,不难求得 的取值范围,即可求出
的取值范围,即可求出 的最小值,并确定取得最小值时的
的最小值,并确定取得最小值时的 的值.
的值.
试题解析:(Ⅰ) 3分
3分
 ,
, 5分
5分
 7分
7分
(Ⅱ)由(Ⅰ)得,
当 时,
时, 9分
9分
 11分
11分
 函数
函数 的最小值为
的最小值为 , 13分
, 13分
且当 ,即
,即 时取到 15分.
时取到 15分.
考点:1.三角函数的图像与性质;2.函数的最值.

练习册系列答案
相关题目