题目内容
（本题满分12分）
已知椭圆C的两焦点分别为
，长轴长为6.
（Ⅰ）求椭圆C的标准方程;
（Ⅱ）已知过点（0，2）且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度.
（Ⅰ）
;（Ⅱ）
.
【解析】
试题分析：（Ⅰ）根据题意可得
,根据
可得
.从而可得椭圆方程.（Ⅱ）由已知可得直线方程.将直线方程与椭圆方程联立,消去
可得关于
的一元二次方程.由韦达定理可得两根之和,两根之积.由两点间距离可得
.
试题解析：【解析】
（Ⅰ）由
，长轴长为6
得：
所以
∴椭圆方程为 5分
（Ⅱ）直线AB的方程为
6分
代入得
设
,∴
10分
又
12分
考点：1椭圆方程;2直线与椭圆的位置关系.
练习册系列答案
相关题目
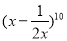的展开式中，x4的系数为( ) 
的图象过定点
，则
的值为 
B．
C．
D．
，则在
时的瞬时速度是 ． 
中，
，前
项之和
，则公比
的值为（ ）
（B）
（C）
或
（D）
或
是正方体
对角线
上一动点，设
的长度为
，若
的面积为
，则
的定义域为R，当
时，
是增函数，则
，
，
的大小关系是( )
B.
D.