题目内容
已知等差数列{an}的前n项和为Sn,且(2n-1)Sn+1-(2n+1)Sn=4n2-1(n∈N*).(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:
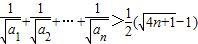 .
.
【答案】分析:(Ⅰ)先由(2n-1)Sn+1-(2n+1)Sn=4n2-1,整理得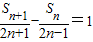 ,进而得
,进而得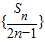 是公差为1的等差数列;求出Sn的表达式,再利用已知前n项和求通项公式的方法即可求出数列{an}的通项公式;
是公差为1的等差数列;求出Sn的表达式,再利用已知前n项和求通项公式的方法即可求出数列{an}的通项公式;
(Ⅱ)先利用(Ⅰ)的结论得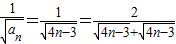 ,再把其放缩到
,再把其放缩到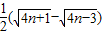 ,代入所求即可证明结论.
,代入所求即可证明结论.
解答:解:(Ⅰ)由(2n-1)Sn+1-(2n+1)Sn=4n2-1,得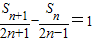 ,
,
∴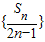 是公差为1的等差数列,
是公差为1的等差数列,
∴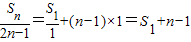 ,Sn=(2n-1)(S1+n-1)①
,Sn=(2n-1)(S1+n-1)①
又∵{an}等差数列,∴a1+a3=2a2,即a1+(S3-S2)=2(S2-S1).
由①得a1+[5(a1+2)-3(a1+1)]=2[3(a1+1)-a1],
解得a1=1,代入①得Sn=2n2-n.
当n≥2时,an=Sn-Sn-1=2n2-n-[2(n-1)2-(n-1)]=4n-3,
上式对n=1也适用,∴an=4n-3.
(Ⅱ)由(Ⅰ)知,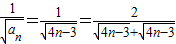
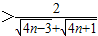
=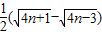 ,
,
∴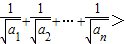
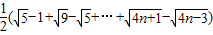
=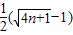 ,故原不等式成立.
,故原不等式成立.
点评:本题主要考查数列递推式以及数列与不等式的综合问题.解决第二问的关键在于把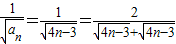 ,放缩到
,放缩到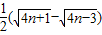 .
.
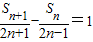 ,进而得
,进而得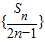 是公差为1的等差数列;求出Sn的表达式,再利用已知前n项和求通项公式的方法即可求出数列{an}的通项公式;
是公差为1的等差数列;求出Sn的表达式,再利用已知前n项和求通项公式的方法即可求出数列{an}的通项公式;(Ⅱ)先利用(Ⅰ)的结论得
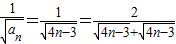 ,再把其放缩到
,再把其放缩到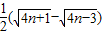 ,代入所求即可证明结论.
,代入所求即可证明结论.解答:解:(Ⅰ)由(2n-1)Sn+1-(2n+1)Sn=4n2-1,得
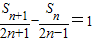 ,
,∴
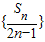 是公差为1的等差数列,
是公差为1的等差数列,∴
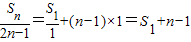 ,Sn=(2n-1)(S1+n-1)①
,Sn=(2n-1)(S1+n-1)①又∵{an}等差数列,∴a1+a3=2a2,即a1+(S3-S2)=2(S2-S1).
由①得a1+[5(a1+2)-3(a1+1)]=2[3(a1+1)-a1],
解得a1=1,代入①得Sn=2n2-n.
当n≥2时,an=Sn-Sn-1=2n2-n-[2(n-1)2-(n-1)]=4n-3,
上式对n=1也适用,∴an=4n-3.
(Ⅱ)由(Ⅰ)知,
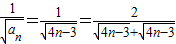
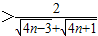
=
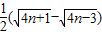 ,
,∴
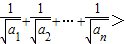
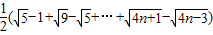
=
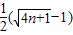 ,故原不等式成立.
,故原不等式成立.点评:本题主要考查数列递推式以及数列与不等式的综合问题.解决第二问的关键在于把
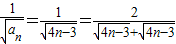 ,放缩到
,放缩到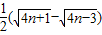 .
. 
练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.