题目内容
已知函数f(x)=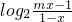 是奇函数.
是奇函数.
(1)求m的值;
(2)解关于x的不等式f-1(x)>b(b∈R,b是常数,b<-1).
解:(1)函数是奇函数,所以f(-x)+f(x)=0恒成立,
所以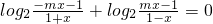 ,
,
即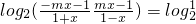 ,
,
即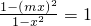 ,
,
所以1-(mx)2=1-x2,
所以m=±1,
当m=1时f(x)=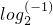 ,无意义,
,无意义,
∴m=-1.
(2)可求得,f-1(x)= ,
,
f-1(x)>b即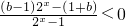 ,
,
令t=2x,t>0,则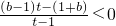 ,
,
即(t-1)[(b-1)t-(1+b)]<0,
它的两个根为t1=1,t2=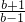 ,
,
当b<-1时,b-1<0,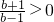 ,t1-t2=1-
,t1-t2=1-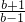 =-
=-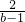 >0,
>0,
∴2x<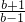 或2x>1,
或2x>1,
∴x<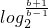 或x>0.
或x>0.
分析:(1)利用函数的奇函数,求出m值即可.
(2)求出反函数,利用f-1(x)>b,通过换元法,结合b的范围,求解不等式即可.
点评:本题考查函数的奇偶性,反函数的知识,含参数的不等式的解法是本题的难点,考查转化思想,计算能力.
所以
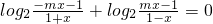 ,
,即
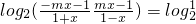 ,
,即
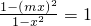 ,
,所以1-(mx)2=1-x2,
所以m=±1,
当m=1时f(x)=
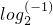 ,无意义,
,无意义,∴m=-1.
(2)可求得,f-1(x)=
 ,
,f-1(x)>b即
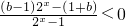 ,
,令t=2x,t>0,则
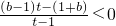 ,
,即(t-1)[(b-1)t-(1+b)]<0,
它的两个根为t1=1,t2=
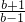 ,
,当b<-1时,b-1<0,
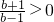 ,t1-t2=1-
,t1-t2=1-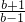 =-
=-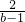 >0,
>0,∴2x<
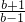 或2x>1,
或2x>1,∴x<
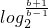 或x>0.
或x>0.分析:(1)利用函数的奇函数,求出m值即可.
(2)求出反函数,利用f-1(x)>b,通过换元法,结合b的范围,求解不等式即可.
点评:本题考查函数的奇偶性,反函数的知识,含参数的不等式的解法是本题的难点,考查转化思想,计算能力.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
已知函数f(x+1)是偶函数,当x2>x1>1时,[f(x2)-f(x1)]( x2-x1)>0恒成立,设a=f (-
),b=f(2),c=f(3),则a,b,c的大小关系为( )
| 1 |
| 2 |
| A、b<a<c |
| B、c<b<a |
| C、b<c<a |
| D、a<b<c |