题目内容
已知![]() 且
且![]() ,
,![]() .
.
(1)求函数![]() 的定义域;
的定义域;
(2)当![]() 时,判断函数
时,判断函数![]() 的单调性,并用函数单调性的定义证明你的结论
的单调性,并用函数单调性的定义证明你的结论
(Ⅰ) ![]() (Ⅱ)
(Ⅱ)![]() 是增函数
是增函数
解析:
(1)由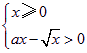 及
及![]() 得
得![]() ,所以
,所以![]() 的定义域为
的定义域为![]()
(2)当![]() 时,函数
时,函数![]() 是增函数
是增函数
设![]() ,则
,则![]() ,
,
因此![]()
![]() ,即
,即![]() ,
,
于是有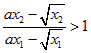 ,又
,又![]() ,……2分 所以有
,……2分 所以有![]()
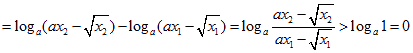 ,
,
即![]() ,所以
,所以![]() 时,函数
时,函数![]() 是增函数
是增函数

练习册系列答案
相关题目
题目内容
已知![]() 且
且![]() ,
,![]() .
.
(1)求函数![]() 的定义域;
的定义域;
(2)当![]() 时,判断函数
时,判断函数![]() 的单调性,并用函数单调性的定义证明你的结论
的单调性,并用函数单调性的定义证明你的结论
(Ⅰ) ![]() (Ⅱ)
(Ⅱ)![]() 是增函数
是增函数
(1)由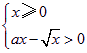 及
及![]() 得
得![]() ,所以
,所以![]() 的定义域为
的定义域为![]()
(2)当![]() 时,函数
时,函数![]() 是增函数
是增函数
设![]() ,则
,则![]() ,
,
因此![]()
![]() ,即
,即![]() ,
,
于是有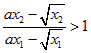 ,又
,又![]() ,……2分 所以有
,……2分 所以有![]()
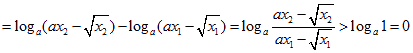 ,
,
即![]() ,所以
,所以![]() 时,函数
时,函数![]() 是增函数
是增函数
