题目内容
函数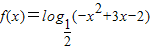
的单调递减区间是 ．
【答案】分析：先求出f（x）的定义域，然后把f（x）分解为两个简单函数y=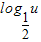
和u=-x2+3x-2，因为y=
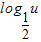单调递减，所以只需求出u=-x2+3x-2的增区间即可．
解答：解：由-x2+3x-2＞0，解得1＜x＜2，所以函数f（x）的定义域为（1，2）．
函数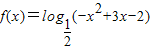
可看作由y=
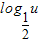和u=-x2+3x-2复合而成的，
在f（x）的定义域内u=-x2+3x-2的增区间是（1，
]，减区间是[
，2），又y=
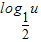单调递减，
所以函数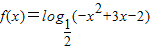
的单调递减区间是（1，
]．
故答案为：（1，
]．
点评：本题考查复合函数的单调性，注意单调区间是函数定义域的子集，故单调区间要在定义域内求解．
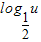和u=-x2+3x-2，因为y=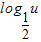单调递减，所以只需求出u=-x2+3x-2的增区间即可．解答：解：由-x2+3x-2＞0，解得1＜x＜2，所以函数f（x）的定义域为（1，2）．
函数
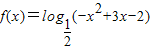可看作由y=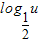和u=-x2+3x-2复合而成的，在f（x）的定义域内u=-x2+3x-2的增区间是（1，
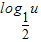]，减区间是[，2），又y=单调递减，所以函数
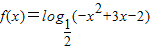的单调递减区间是（1，]．故答案为：（1，
]．点评：本题考查复合函数的单调性，注意单调区间是函数定义域的子集，故单调区间要在定义域内求解．
练习册系列答案
相关题目
的单调递减区间是 . 
的单调递减区间是 . (科网