题目内容
设f(x)=
,函数图象与x轴围成封闭区域的面积为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:利用坐标系中作出函数图象的形状,通过定积分的公式,分别对两部分用定积分求出其面积,再把它们相加,即可求出围成的封闭区域曲边图形的面积.
解答:解:根据题意作出函数的图象:
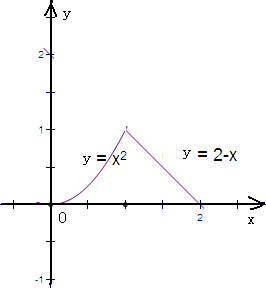
根据定积分,得所围成的封闭区域的面积S=
x2dx+∫
-(2-x)dx=
+(2-
) =
故选C
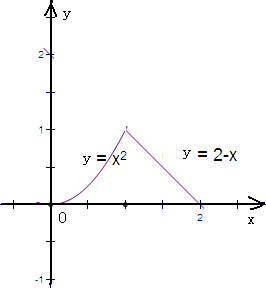
根据定积分,得所围成的封闭区域的面积S=
| ∫ | 1 0 |
2 1 |
| 1 |
| 3 |
| 3 |
| 2 |
| 5 |
| 6 |
故选C
点评:本题考查分段函数的图象和定积分的运用,考查积分与曲边图形面积的关系,属于中档题.解题关键是找出被积函数的原函数,注意运算的准确性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
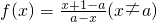
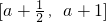 时,求f(x)的值域;
时,求f(x)的值域;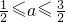 ,求g(x)的最小值.
,求g(x)的最小值.