题目内容
(本小题满分12分)
已知椭圆
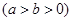 的离心率为
的离心率为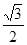 ,直线
,直线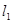 经过椭圆的上顶点
经过椭圆的上顶点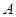 和右顶点
和右顶点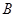 ,并且和圆
,并且和圆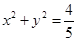 相切.
相切.
(1)求椭圆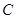 的方程;
的方程;
(2)设直线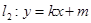
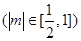 与椭圆
与椭圆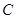 相交于
相交于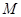 ,
,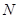 两点,以线段
两点,以线段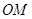 ,
, 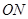 为邻边作平行四边行
为邻边作平行四边行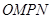 ,其中顶点
,其中顶点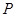 在椭圆
在椭圆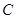 上,
上,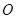 为坐标原点,求
为坐标原点,求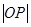 的取值范围.
的取值范围.
【答案】
(1)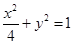 ;(2)
;(2)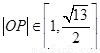 。
。
【解析】本试题主要是考查了圆锥曲线方程的求解以及直线与圆锥曲线的位置关系的综合运用。体现了运用代数的方法解决解析几何的本质思想
(1)由题意的几何性质和点到直线的距离得到a,b,c的关系式,从而得到椭圆方程的求解。
(2)因为设直线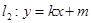
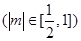 与椭圆
与椭圆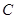 相交于
相交于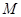 ,
,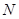 两点,以线段
两点,以线段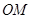 ,
, 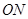 为邻边作平行四边行
为邻边作平行四边行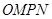 ,那么联立方程组,借助于韦达定理和两点距离公式得到OP的范围。
,那么联立方程组,借助于韦达定理和两点距离公式得到OP的范围。
解答:(1)由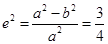 得
得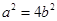 ,所以
,所以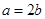 ……………………1分
……………………1分
所以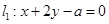 ,有
,有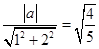 ,解得
,解得 ………..5分
………..5分
所以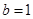 ,所以椭圆方程为
,所以椭圆方程为 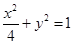 …………………………….6分
…………………………….6分
(2)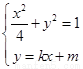 , 消去
, 消去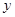 得:
得:
设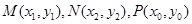
则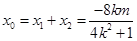 ,
, 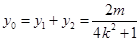 ,
,
故点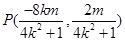 …………………………………………………9分
…………………………………………………9分
点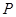 在椭圆上,有
在椭圆上,有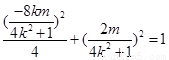 ,整理得
,整理得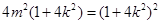
所以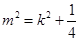 ,
,
而 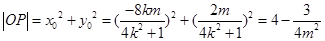 ,………….11分
,………….11分
因为  ,所以
,所以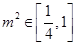 ,所以
,所以
 ,
,
所以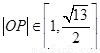 …………………………………………………………….12分
…………………………………………………………….12分

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目