Question

（本小题满分12分）

已知函数，其中.

（Ⅰ）求函数的单调区间；

（Ⅱ）若直线是曲线的切线，求实数的值；

（Ⅲ）设，求在区间上的最大值.

（其中为自然对数的底数）

Answer 1

解：（Ⅰ），（），                                 ……3分

在区间和上，；在区间上，.

所以，的单调递减区间是和，单调递增区间是.   ……4分

（Ⅱ）设切点坐标为，则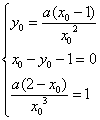          ……7分（1个方程1分）

解得，.                                               ……8分

（Ⅲ），

则，                                       

解，得，

所以，在区间上，为递减函数，

在区间上，为递增函数.                      ……9分

当，即时，在区间上，为递增函数，

所以最大值为.                      ……10分

当，即时，在区间上，为递减函数，

所以最大值为.                             ……11分

当，即时，的最大值为和中较大者；

，解得，

所以，时，最大值为，       

时，最大值为.                ……12分

综上所述，当时，最大值为，当时，的最大值为.