题目内容
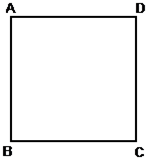正方形ABCD的边长为1，记| AB |
| a |
| AD |
| b |
| BD |
| c |
（1）求作
| a |
| b |
| c |
| a |
| b |
| c |
（2）求|
| AB |
| BC |
| CD |
| DA |
| AB |
| BC |
| DC |
| AD |
分析：（1）根据向量加法的平行四边形法则三角形法则和相等向量，作出
+
+
，-
-
+
；
（2）利用向量加法的三角形法则，|
+
+
+
|和|
+
+
+
|进行化简，再求其值即可．
| a |
| b |
| c |
| a |
| b |
| c |
（2）利用向量加法的三角形法则，|
| AB |
| BC |
| CD |
| DA |
| AB |
| BC |
| DC |
| AD |
解答：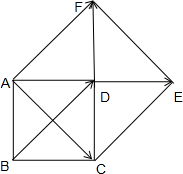
解：（1）①连接AC，则
+
=
，
②过点A做
=
，
③以AC、AF为邻边作平行四边形ACEF，则
=
+
+
，
=-
-
+
；
（2）
+
+
+
|=|
|=0，
|
+
+
+
|=|
+
|=2
．
解：（1）①连接AC，则| a |
| b |
| AC |
②过点A做
| AF |
| BD |
③以AC、AF为邻边作平行四边形ACEF，则
| AE |
| a |
| b |
| c |
| DF |
| a |
| b |
| c |
（2）
| |AB |
| BC |
| CD |
| DA |
| 0 |
|
| AB |
| BC |
| DC |
| AD |
| AC |
| AC |
| 2 |
点评：此题考查向量加法减法的运算以及其几何意义，熟记基础知识是解题的关键，体现了数形结合的思想，属基础题．
练习册系列答案
精英口算卡系列答案
相关题目
如图，正方形ABCD的边长为1，正方形ADEF所在平面与平面ABCD互相垂直，G，H是DF，FC的中点．