题目内容
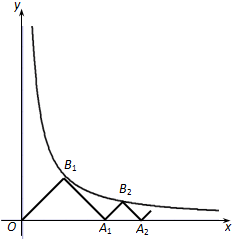 设函数y=
设函数y=| 1 |
| x |
| 1 |
| x |
(1)求a1,并求出an与an-1之间的关系式;
(2)求数列{an}的通项公式;
(3)bn=
| 2 |
| an-1+an |
分析:(1)由题意,a1=
+
,可得a1的值,求出Bn的坐标,代入曲线方程,可得结论;
(2)确定数列{an2}是首项为4,公差为4的等差数列,可求数列{an}的通项公式;
(3)确定通项,利用累加法可求和.
| a1 |
| 2 |
| 2 |
| a1 |
(2)确定数列{an2}是首项为4,公差为4的等差数列,可求数列{an}的通项公式;
(3)确定通项,利用累加法可求和.
解答:解:(1)由题意,a1=
+
,解得a1=2.
过Bn点作BnH⊥x轴,垂足为H,
∵△An-1BnAn为等腰直角三角形,且Bn为直角顶点,
∴|BnH|=
|An-1An|=
,
∴Bn点的纵坐标为
,
∵△An-1BnAn为等腰直角三角形,且Bn为直角顶点,
∴H点为线段An-1An的中点,
∴H点横坐标为
,
∵BnH⊥x轴,∴Bn点的横坐标也为
,
∵Bn点为函数y=
(x>0)图象上的点,
∴
•
=1
∴an2-an-12=4.
(2)∵an2-an-12=4,a1=2,
∴数列{an2}是首项为4,公差为4的等差数列,
∴an2=4n,
∴an=2
.
(3)∵bn=
=
=
-
,
∴Sn=(
-0)+(
-
)+…+(
-
)=
.
| a1 |
| 2 |
| 2 |
| a1 |
过Bn点作BnH⊥x轴,垂足为H,
∵△An-1BnAn为等腰直角三角形,且Bn为直角顶点,
∴|BnH|=
| 1 |
| 2 |
| an-an-1 |
| 2 |
∴Bn点的纵坐标为
| an-an-1 |
| 2 |
∵△An-1BnAn为等腰直角三角形,且Bn为直角顶点,
∴H点为线段An-1An的中点,
∴H点横坐标为
| an+an-1 |
| 2 |
∵BnH⊥x轴,∴Bn点的横坐标也为
| an+an-1 |
| 2 |
∵Bn点为函数y=
| 1 |
| x |
∴
| an+an-1 |
| 2 |
| an-an-1 |
| 2 |
∴an2-an-12=4.
(2)∵an2-an-12=4,a1=2,
∴数列{an2}是首项为4,公差为4的等差数列,
∴an2=4n,
∴an=2
| n |
(3)∵bn=
| 2 |
| an-1+an |
| 1 | ||||
|
| n |
| n-1 |
∴Sn=(
| 1 |
| 2 |
| 1 |
| n |
| n-1 |
| n |
点评:本题考查数列的通项公式和前n项和公式的求法,考查函数与数列知识的综合,确定数列的通项是关键.

练习册系列答案
相关题目
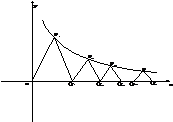 P1,P2,…,Pn…顺次为函数
P1,P2,…,Pn…顺次为函数