题目内容
在等差数列{an}中,a1=1,a5=9,在数列{bn}中,b1=2,且bn=2bn-1-1,(n≥2)
(1)求数列{an}和{bn}的通项公式;
(2)设 ,求Tn.
,求Tn.
解:(1)由等差数列的通项公式可得,d=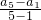 =2
=2
∴an=1+2(n-1)=2n-1
由bn=2bn-1-1可得bn-1=2(bn-1-1)(n≥2)
∴{bn-1}是以b1-1=1为首项,2为公比的等比数列
∴bn-1=2n-1
故bn=2n-1+1
(2) =
=
= ①
①
则 ②
②
①-②可得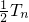 =
=

=
=
= =
=
所以
分析:(1)由已知可求公差d,代入等差数列的通项公式可求an,由bn=2bn-1-1可得bn-1=2(bn-1-1)(n≥2),则可得{bn-1}是等比数列,结合等比数列的通项公式可求bn
(2)由(1)可得Tn═ ,结合所求和的特点,考虑利用错位相减求解.
,结合所求和的特点,考虑利用错位相减求解.
点评:本题主要考查了等差数列的通项公式的应用,构造等比求数列的通项公式,错位相减求数列的和是数列求和中的重点与难点.
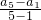 =2
=2∴an=1+2(n-1)=2n-1
由bn=2bn-1-1可得bn-1=2(bn-1-1)(n≥2)
∴{bn-1}是以b1-1=1为首项,2为公比的等比数列
∴bn-1=2n-1
故bn=2n-1+1
(2)
 =
=
=
 ①
①则
 ②
②①-②可得
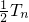 =
=

=

=

=
 =
=
所以

分析:(1)由已知可求公差d,代入等差数列的通项公式可求an,由bn=2bn-1-1可得bn-1=2(bn-1-1)(n≥2),则可得{bn-1}是等比数列,结合等比数列的通项公式可求bn
(2)由(1)可得Tn═
 ,结合所求和的特点,考虑利用错位相减求解.
,结合所求和的特点,考虑利用错位相减求解.点评:本题主要考查了等差数列的通项公式的应用,构造等比求数列的通项公式,错位相减求数列的和是数列求和中的重点与难点.

练习册系列答案
相关题目