题目内容
已知函数 .
.
(Ⅰ)若 时,求
时,求 的值域;
的值域;
(Ⅱ)若存在实数 ,当
,当 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【答案】
(I) 的值域为:
的值域为: .(II)
.(II) .
.
【解析】
试题分析:(I)将二次函数 配方,结合抛物线的图象便可得
配方,结合抛物线的图象便可得 的值域.
的值域.
(II)由 恒成立得:
恒成立得: 恒成立,
恒成立,
令 ,
, 则只需
则只需 的最大值小于等于0.
的最大值小于等于0.
由此得: ,令
,令
则原题可转化为:存在 ,使得
,使得 .这又需要
.这又需要 时
时 .接下来又对二次函数
.接下来又对二次函数 分情况讨论,从而求出实数
分情况讨论,从而求出实数 的取值范围.
的取值范围.
试题解析:(I)将二次函数 配方得:
配方得: 2分
2分
该函数的图象是一条开口向上的抛物线,顶点为 ,
, .
.
因为 ,所以
,所以 最大值为
最大值为 ,
,
∴ 的值域为:
的值域为: 6分
6分
(II)由 恒成立得:
恒成立得: 恒成立,
恒成立,
令 ,
, 因为抛物线的开口向上,所以
因为抛物线的开口向上,所以 ,由
,由 恒成立知:
恒成立知: 8分
8分
化简得: 令
令
则原题可转化为:存在 ,使得
,使得 即:当
即:当 ,
, 10分
10分
∵ ,
, 的对称轴:
的对称轴:
 即:
即: 时,
时,
∴
 解得:
解得:
②当 即:
即: 时,
时,
∴
 解得:
解得:
综上: 的取值范围为:
的取值范围为: 13分
13分
法二:也可 ,
,
化简得: 有解.
有解.
 ,则
,则 .
.
考点:1、二次函数;2、函数的最值;3、解不等式.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 ,若
,若 ,则实数
,则实数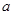 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
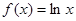 ,若
,若
 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间 上有两个零点,求实数b的取值范围;
上有两个零点,求实数b的取值范围;
 ,若
,若 为奇函数,则
为奇函数,则 ▲
▲
 ,若
,若 ,
, ,则
,则  (B)
(B)
 (D)
(D) 与
与 的大小不能确定
的大小不能确定