题目内容
已知函数 .
.(Ⅰ)求函数G(x)=h(x)+f(x)的单调区间;
(Ⅱ)当a=2,问是否存在实数t>0,使得函数F(x)=h(x)-tg(x)+f(x)有两个相异的零点?若存在,请求出t的取值范围;若不存在,说明理由.
【答案】分析:(Ⅰ)分别把f(x)和h(x)的解析式代入G(x)中,求出函数的定义域及G′(x)=0时x的值,令导函数大于0解出x的范围即为函数的增区间,令导函数小于0求出x的值即为函数的减区间;
(II)先假设存在t符合条件,根据题意求出F(x)的解析式和定义域,再进行求导并对其整理,再由定义域和条件进行转化: 有两个相异的正实根,利用韦达定理表示出两根之和、积,并判断出符号,再对t分类讨论进行说明.
有两个相异的正实根,利用韦达定理表示出两根之和、积,并判断出符号,再对t分类讨论进行说明.
解答:解:(Ⅰ)由题意 ,
,
∴G(x)的定义域为 ,
,
 =
= ,
,
由G′(x)=0得, ,
,
 ,∴
,∴ ,
,
∴ ,
, ,
,
由G′(x)>0得,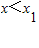 或
或 ;由G′(x)>0得,
;由G′(x)>0得, ,且x≠0,
,且x≠0,
∴G(x)在 上是增函数,
上是增函数,
在 上是减函数;
上是减函数;
(Ⅱ)假设存在实数t>0,使得函数 (x>0)有
(x>0)有
相异的零点为x1,x2,则x1>0,x2>0,
∴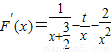 =
=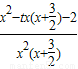 =
= ,
,
令y= ,
,
由题意得,F′(x)=0有两个相异的正实根,
即 有两个相异的正实根,
有两个相异的正实根,
∴t≠1,且 ,
,
∴当0<t<1时,有1-t>0,则 ,故舍去;
,故舍去;
当t>1时,有1-t<0,则 ,故舍去,
,故舍去,
综上,不存在t>0满足条件.
点评:本题考查利用导数研究函数的单调性,考查存在性问题,突出考查构造函数与转化,分类讨论数学思想及综合分析与运算的能力,属于难题.
(II)先假设存在t符合条件,根据题意求出F(x)的解析式和定义域,再进行求导并对其整理,再由定义域和条件进行转化:
 有两个相异的正实根,利用韦达定理表示出两根之和、积,并判断出符号,再对t分类讨论进行说明.
有两个相异的正实根,利用韦达定理表示出两根之和、积,并判断出符号,再对t分类讨论进行说明.解答:解:(Ⅰ)由题意
 ,
,∴G(x)的定义域为
 ,
, =
= ,
,由G′(x)=0得,
 ,
, ,∴
,∴ ,
,∴
 ,
, ,
,由G′(x)>0得,
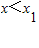 或
或 ;由G′(x)>0得,
;由G′(x)>0得, ,且x≠0,
,且x≠0,∴G(x)在
 上是增函数,
上是增函数,在
 上是减函数;
上是减函数;(Ⅱ)假设存在实数t>0,使得函数
 (x>0)有
(x>0)有相异的零点为x1,x2,则x1>0,x2>0,
∴
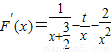 =
=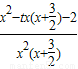 =
= ,
,令y=
 ,
,由题意得,F′(x)=0有两个相异的正实根,
即
 有两个相异的正实根,
有两个相异的正实根,∴t≠1,且
 ,
,∴当0<t<1时,有1-t>0,则
 ,故舍去;
,故舍去;当t>1时,有1-t<0,则
 ,故舍去,
,故舍去,综上,不存在t>0满足条件.
点评:本题考查利用导数研究函数的单调性,考查存在性问题,突出考查构造函数与转化,分类讨论数学思想及综合分析与运算的能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数 .
.
(1)求 的最小值;
的最小值;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间.设 ,试问函数
,试问函数 在
在 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数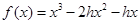 ,若
,若 且
且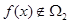 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得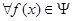 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


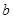
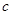




 ,编写一个程序求函数值.
,编写一个程序求函数值. 试画出求函数值的程序框图.
试画出求函数值的程序框图.