题目内容
已知函数f(x)=ax+ +c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
(I)用a表示出b,c;
(II)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围.
y解:(Ⅰ)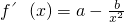 ,
,
则有 ,
,
解得
(Ⅱ)由(Ⅰ)知, ,
,
令g(x)=f(x)-lnx=ax+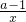 +1-2a-lnx,x∈[1,+∞)
+1-2a-lnx,x∈[1,+∞)
则g(l)=0,
(i)当 ,
,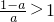
若 ,则g′(x)<0,g(x)是减函数,
,则g′(x)<0,g(x)是减函数,
所以g(x)<g(l)=0,f(x)>lnx,故f(x)≥lnx在[1,+∞)上恒不成立.
(ii) 时,
时,
若f(x)>lnx,故当x≥1时,f(x)≥lnx
综上所述,所求a的取值范围为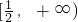
分析:(I)根据导数的几何意义求出函数f(x)在x=1处的导数,从而求得切线的斜率,以及切点在函数f(x)的图象上,建立方程组,解之即可;
(II)先构造函数g(x)=f(x)-lnx=ax+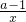 +1-2a-lnx,x∈[1,+∞),利用导数研究g(x)的最小值,讨论a的范围,分别进行求解即可求出a的取值范围.
+1-2a-lnx,x∈[1,+∞),利用导数研究g(x)的最小值,讨论a的范围,分别进行求解即可求出a的取值范围.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数恒成立问题等基础题知识,考查运算求解能力,考查化归与转化思想,分类讨论思想,属于基础题.
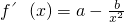 ,
,则有
 ,
,解得

(Ⅱ)由(Ⅰ)知,
 ,
,令g(x)=f(x)-lnx=ax+
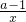 +1-2a-lnx,x∈[1,+∞)
+1-2a-lnx,x∈[1,+∞)则g(l)=0,

(i)当
 ,
,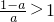
若
 ,则g′(x)<0,g(x)是减函数,
,则g′(x)<0,g(x)是减函数,所以g(x)<g(l)=0,f(x)>lnx,故f(x)≥lnx在[1,+∞)上恒不成立.
(ii)
 时,
时,
若f(x)>lnx,故当x≥1时,f(x)≥lnx
综上所述,所求a的取值范围为
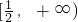
分析:(I)根据导数的几何意义求出函数f(x)在x=1处的导数,从而求得切线的斜率,以及切点在函数f(x)的图象上,建立方程组,解之即可;
(II)先构造函数g(x)=f(x)-lnx=ax+
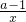 +1-2a-lnx,x∈[1,+∞),利用导数研究g(x)的最小值,讨论a的范围,分别进行求解即可求出a的取值范围.
+1-2a-lnx,x∈[1,+∞),利用导数研究g(x)的最小值,讨论a的范围,分别进行求解即可求出a的取值范围.点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数恒成立问题等基础题知识,考查运算求解能力,考查化归与转化思想,分类讨论思想,属于基础题.

练习册系列答案
相关题目