题目内容
已知等差数列![]() 中,
中,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)调整数列![]() 的前三项
的前三项![]() 的顺序,使它成为等比数列
的顺序,使它成为等比数列![]() 的前三项,求
的前三项,求![]() 的前
的前![]() 项和.
项和.
解:(1)由已知,得求得![]() ,
,![]()
∴![]() 的公差d=3 ∴an=a1+(n-1)d=-2+3(n-1)=3n-5.
的公差d=3 ∴an=a1+(n-1)d=-2+3(n-1)=3n-5.
(2)由(1),得a3=a2+d=1+3=4,∴a1=-2,a2=1,a3=4.
依题意可得:数列{bn}的前三项为
b1=1,b2=-2,b3=4或b1==4,b2=-2,b3=1
(i)当数列{bn}的前三项为b1=1,b2=-2,b3=4时,则q=-2 .
![]() .
.
(ii)当数列{bn}的前三项为b1=4,b2=-2,b3=1时,则
![]() .
. 

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 中,
中, 的值是( )
的值是( ) B.
B.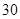 C.
C.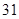 D.
D.
 中,
中, 的值是 (
)
的值是 (
)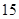 B.
B.
 C.
31 D. 64
C.
31 D. 64 }中,
}中, ,设
,设 求:
求: .
. 中,
中, ,记
,记 ,则
,则 的值为( )
的值为( )