Question

已知数列{a_n}的前n项和为S_n,又有数列{b_n},它们满足关系b₁=a₁,对于n∈N^*有a_n+S_n=n,b_n+1=a_n+1-a_n,求证{b_n}是等比数列,并求其通项公式.

Answer 1

证明:因为a_n+S_n=n,                                              ①

    所以a_n-1+S_n-1=(n-1)(n≥2).                            ②

    所以①-②得a_n-a_n-1+a_n=1,

    即a_n=(a_n-1+1)(n≥2).

    又b_n+1=a_n+1-a_n=(a_n+1)-a_n=(1-a_n),

    所以==

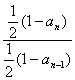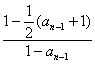
    =(n≥2).

    由a_n+S_n=n可得a₁+S₁=a₁+a₁=1.

    所以a₁==b₁.

    所以b₂=(1-a₁)= ·=b₁·.

    故=对于n∈N^*均成立,那么数列{b_n}是等比数列,其通项b_n=b₁()^n-1=.

讲评:等比数列的判定方法主要有:

    (1)定义法:=q(q是不为0的常数,n∈N^*){a_n}是等比数列;

    (2)通项公式法:a_n=cqⁿ(c、q均是不为0的常数,n∈N^*){a_n}是等比数列;

    (3)等比中项公式法:a_n+1²=a_n·a_n+2(a_n、a_n+1、a_n+2不为零,n∈N^*){a_n}是等比数列.