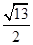题目内容
设A（3，3，1）、B（1，0，5）、C（0，1，0），则AB的中点M到C点的距离为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析：先由中点坐标公式求得AB的中点M的空间直角坐标，再利用空间坐标系中两点间的距离公式求出M到C点的距离即可．
解答：解：∵A（3，3，1）、B（1，0，5）
∴AB的中点M坐标为：（2，
，3），
又∵C（0，1，0），
∴M到C点的距离为：
d=
=
．
故选C．
∴AB的中点M坐标为：（2，
| 3 |
| 2 |
又∵C（0，1，0），
∴M到C点的距离为：
d=
(2-0)2+(
|
| ||
| 2 |
故选C．
点评：本小题主要考查空间直角坐标系、距离公式等基础知识，考查点、线、面间的距离计算，考查空间想象力、化归与转化思想．属于基础题．
练习册系列答案
相关题目
B．
C．
D．
B．
C．
D．
设A是由m×n个实数组成的m行n列的数表，满足：每个数的绝对值不大于1，且所有数的和为零，记s(m，n)为所有这样的数表构成的集合。
对于A∈S(m,n),记ri(A)为A的第ⅰ行各数之和（1≤ⅰ≤m），Cj(A)为A的第j列各数之和（1≤j≤n）：
记K(A)为∣r1(A)∣,∣R2(A)∣,…,∣Rm(A)∣,∣C1(A)∣,∣C2(A)∣,…,∣Cn(A)∣中的最小值。
（1） 对如下数表A，求K（A）的值；
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
（2）设数表A∈S（2,3）形如
|
1 |
1 |
c |
|
a |
b |
-1 |
求K（A）的最大值；
（3）给定正整数t，对于所有的A∈S（2,2t+1），求K（A）的最大值。
【解析】（1）因为
，
所以
（2） 不妨设
.由题意得
.又因为
，所以
，
于是
，
，
所以
，当
，且
时，
取得最大值1。
（3）对于给定的正整数t，任给数表
如下，
|
|
|
… |
|
|
|
|
… |
|
任意改变A的行次序或列次序，或把A中的每一个数换成它的相反数，所得数表
，并且
，因此，不妨设
，
且
。
由
得定义知，
，
又因为
所以
所以，
对数表
：
|
1 |
1 |
… |
1 |
|
… |
|
|
|
|
… |
|
-1 |
… |
-1 |
则
且
，
综上，对于所有的，的最大值为