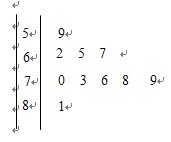题目内容
.已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A和63000单位维生素B.
| | 甲 | 乙 | 丙 |
| 维生素A(单位/千克) | 600 | 700 | 400 |
| 维生素B(单位/千克) | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
(Ⅱ)确定x,y,z的值,使成本最低.
解:(1)依题意,得
 .
.
(2)由 , 得
, 得 ,
,

当且仅当 时等号成立.
时等号成立.
∴当x=50千克,y=20千克,z=30千克时,混合物成本最低为850元.
解析

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
本小题满分12分)
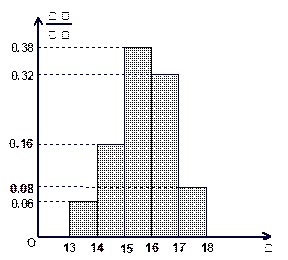
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组 ,第二组
,第二组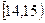 ……第五组
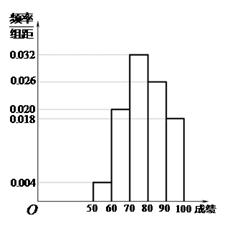
……第五组 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.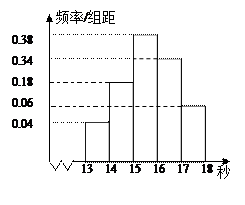
(Ⅰ)求这组数据的众数和中位数(精确到0.1);
(II)设 表示样本中两个学生的百米测
表示样本中两个学生的百米测
试成绩,已知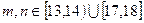
求事件“ ”的概率.
”的概率.
(Ⅲ) 根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如下 表
表
| 性别 是否达标 | 男 | 女 | 合计 |
| 达标 | 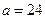 | 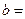 ______ ______ | _____ |
| 不达标 | 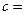 _____ _____ | 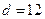 | _____ |
| 合计 | ______ | ______ | 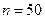 |
(本小题满分12分)
甲乙两个学校高三年级分别为1100人,1000人,为了统计两个学校在地区二模考试的数学科目成绩,采用分层抽样抽取了105名学生的成绩,并作出了部分频率分布表如下:(规定考试成绩在[120,150]内为优秀)
甲校:
| 分组 | 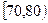 | 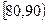 | 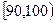 |  | 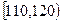 | 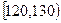 | 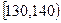 | [140,150] |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | 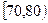 | 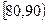 | 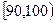 |  | 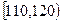 | 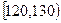 | 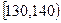 | [140,150] |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(2)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
| | 甲校 | 乙校 | 总计 |
| 优秀 | | | |
| 非优秀 | | | |
| 总计 | | | |
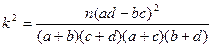
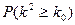 | 0.10 | 0.025 | 0.010 |
 | 2.706 | 5.024 | 6.635 |
已知x与y之间的一组数据
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
(2)若
 x与y线性相关,写出线性回归方程必定经过的点
x与y线性相关,写出线性回归方程必定经过的点(3)若x与y线性相关求出线性回归方程,
(4)说出2个刻画回归效果的手段,假设R
 =0.74
=0.74 说明什么问题。
说明什么问题。参考公式
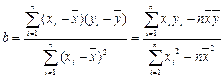
 级的
级的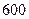 名学生参加一次科普知识竞赛,然后随机抽取
名学生参加一次科普知识竞赛,然后随机抽取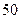 名学生的成绩进行统计分析.
名学生的成绩进行统计分析.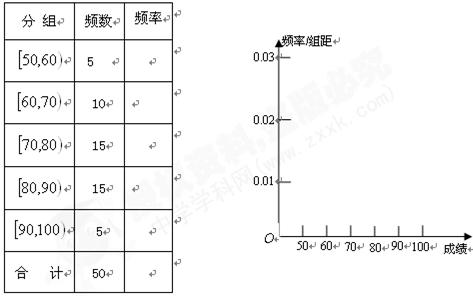
 表示抽取的3名学生中男学生数,求
表示抽取的3名学生中男学生数,求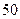 名学生在一次百米测试中,成绩全部介于
名学生在一次百米测试中,成绩全部介于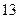 秒与
秒与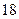 秒之间,将测
秒之间,将测 试结果按如下方式分成五组:第一组
试结果按如下方式分成五组:第一组 ,第二组
,第二组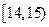 ,…,第五组
,…,第五组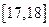 ,下图是按上述分组方法得到的频率分布直方图。
,下图是按上述分组方法得到的频率分布直方图。 秒且小于
秒且小于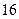 秒认为良好,求该班在这次百米测试中成绩良好的人数;
秒认为良好,求该班在这次百米测试中成绩良好的人数;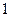 的概率。
的概率。