题目内容
已知向量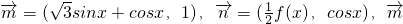 ∥
∥ .
.
(I)求f(x)的单调增区间及在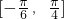 内的值域;
内的值域;
(II)已知A为△ABC的内角,若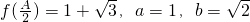 ,求△ABC的面积.
,求△ABC的面积.
解:∵
∴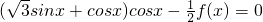
∴f(x)=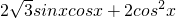 =
=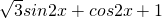
=2sin(2x )+1
)+1
(1)令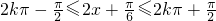 可得
可得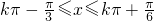 ,k∈Z
,k∈Z
∴f(x)的单调增区间为[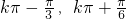 ]k∈Z
]k∈Z
由所求函数的单调递增区间可知,函数在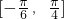 单调递增
单调递增
∴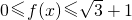
(2)由题意可得,f(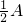 )=2sin(A+
)=2sin(A+ )+1=1+
)+1=1+
∴sin(A+ )=
)=
∵A∈(0,π)
∴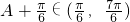
∴A+ =
= 或
或
∴A= 或
或
∵a=1<b=
∴A=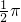 不合题意
不合题意
当A= 时,由正弦定理可得,sinB=
时,由正弦定理可得,sinB=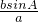 =
=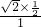 =
=
∵a<b
∴A<B
∴B= 或
或
当A= ,B=
,B= 时,C=
时,C= ,此时S△ABC=
,此时S△ABC=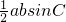 =
=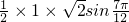 =
=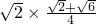 =
=
当A= ,B=
,B= 时,C=
时,C= ,此时S△ABC=
,此时S△ABC=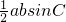 =
=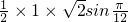 =
=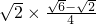 =
=
分析:由 ,根据向量平行的坐标表示整理可求f(x)=2sin(2x
,根据向量平行的坐标表示整理可求f(x)=2sin(2x )+1
)+1
(1)令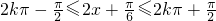 可求函数的单调增区间,由所求函数的单调递增区间可求函数在
可求函数的单调增区间,由所求函数的单调递增区间可求函数在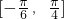 单调性,进而可求函数的值域
单调性,进而可求函数的值域
(2)由题f(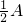 )=1+
)=1+ 及a<b可求A,然后由正弦定理可得,sinB=
及a<b可求A,然后由正弦定理可得,sinB=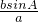 可求B,进而可求C,代入三角形的面积公式S△ABC=
可求B,进而可求C,代入三角形的面积公式S△ABC=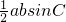 可求
可求
点评:本题主要考查了向量平行的坐标表示的应用,三角函数的辅助角公式及正弦函数的性质、三角形的面积公式等知识的综合应用,具有一定的 综合性

∴
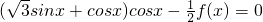
∴f(x)=
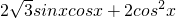 =
=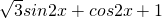
=2sin(2x
 )+1
)+1(1)令
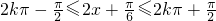 可得
可得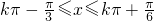 ,k∈Z
,k∈Z∴f(x)的单调增区间为[
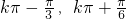 ]k∈Z
]k∈Z由所求函数的单调递增区间可知,函数在
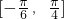 单调递增
单调递增∴
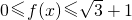
(2)由题意可得,f(
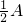 )=2sin(A+
)=2sin(A+ )+1=1+
)+1=1+
∴sin(A+
 )=
)=
∵A∈(0,π)
∴
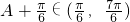
∴A+
 =
= 或
或
∴A=
 或
或
∵a=1<b=

∴A=
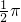 不合题意
不合题意当A=
 时,由正弦定理可得,sinB=
时,由正弦定理可得,sinB=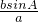 =
=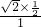 =
=
∵a<b
∴A<B
∴B=
 或
或
当A=
 ,B=
,B= 时,C=
时,C= ,此时S△ABC=
,此时S△ABC=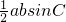 =
=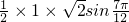 =
=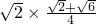 =
=
当A=
 ,B=
,B= 时,C=
时,C= ,此时S△ABC=
,此时S△ABC=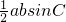 =
=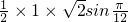 =
=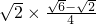 =
=
分析:由
 ,根据向量平行的坐标表示整理可求f(x)=2sin(2x
,根据向量平行的坐标表示整理可求f(x)=2sin(2x )+1
)+1(1)令
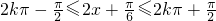 可求函数的单调增区间,由所求函数的单调递增区间可求函数在
可求函数的单调增区间,由所求函数的单调递增区间可求函数在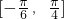 单调性,进而可求函数的值域
单调性,进而可求函数的值域(2)由题f(
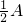 )=1+
)=1+ 及a<b可求A,然后由正弦定理可得,sinB=
及a<b可求A,然后由正弦定理可得,sinB=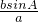 可求B,进而可求C,代入三角形的面积公式S△ABC=
可求B,进而可求C,代入三角形的面积公式S△ABC=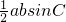 可求
可求点评:本题主要考查了向量平行的坐标表示的应用,三角函数的辅助角公式及正弦函数的性质、三角形的面积公式等知识的综合应用,具有一定的 综合性

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
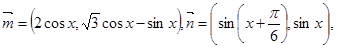 且满足
且满足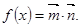
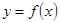 的单调递增区间;
的单调递增区间;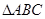 的内角A满足
的内角A满足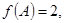 且
且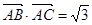 ,求边BC的最小值.
,求边BC的最小值.
 ,定义
,定义
 的单调递减区间;
的单调递减区间; 为偶函数,求
为偶函数,求 的值。
的值。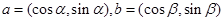 ,且
,且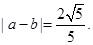
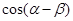 的值;
的值;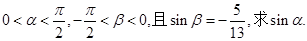
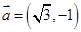 ,
,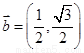 ,
, 平行的单位向量
平行的单位向量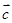 ;
;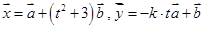 ,若存在
,若存在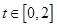 使得
使得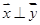 成立,求
成立,求 的取值范围。
的取值范围。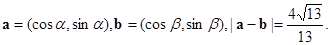 [来源:ZXXK]
[来源:ZXXK]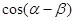 的值;[来源:学|科|网]
的值;[来源:学|科|网] 的值.
的值.