题目内容
已知双曲线c：
，以右焦点F为圆心，|OF|为半径的圆交双曲线两渐近线于点M、N （异于原点O），若|MN|=
，则双曲线C的离心率 是（ ）A．
B．
C．2
D．
【答案】分析：连接NF，设MN交x轴于点B，根据双曲线渐近线方程结合图形的对称性，求出N（
，
），再由|NF|=c在Rt△BNF中利用勾股定理建立关于a、b、c的关系式，化简整理可得c=2a，由此即可得到该双曲线的离心率．
解答：解：
连接NF，设MN交x轴于点B
∵⊙F中，M、N关于OF对称，
∴∠NBF=90°且|BN|=
|MN|=
=
，
设N（m，
），可得
=
，得m=
Rt△BNF中，|BF|=c-m=
∴由|BF|2+|BN|2=|NF|2，得（
）2+（
）2=c2
化简整理，得b=
c，可得a=
，故双曲线C的离心率e=
=2
故选：C
点评：本题给出以双曲线右焦点F为圆心的圆过坐标原点，在已知圆F被两条渐近线截得弦长的情况下求双曲线的离心率，着重考查了双曲线的标准方程与简单几何性质、直线与圆的位置关系等知识，属于基础题．
，），再由|NF|=c在Rt△BNF中利用勾股定理建立关于a、b、c的关系式，化简整理可得c=2a，由此即可得到该双曲线的离心率．解答：解：
连接NF，设MN交x轴于点B∵⊙F中，M、N关于OF对称，
∴∠NBF=90°且|BN|=
|MN|==，设N（m，
），可得=，得m=Rt△BNF中，|BF|=c-m=
∴由|BF|2+|BN|2=|NF|2，得（
）2+（）2=c2化简整理，得b=
c，可得a=，故双曲线C的离心率e==2故选：C
点评：本题给出以双曲线右焦点F为圆心的圆过坐标原点，在已知圆F被两条渐近线截得弦长的情况下求双曲线的离心率，着重考查了双曲线的标准方程与简单几何性质、直线与圆的位置关系等知识，属于基础题．
练习册系列答案
相关题目
，以C的右焦点为圆心且与C的渐近线相切的圆的半径是（ ）
（D ）
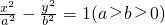，以右焦点F为圆心，|OF|为半径的圆交双曲线两渐近线于点M、N （异于原点O），若|MN|=
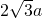，则双曲线C的离心率 是
，以C的右焦点为圆心且与C的渐近线相切的圆的半径是 ．
，以右焦点F为圆心，|OF|为半径的圆交双曲线两渐近线于点M、N （异于原点O），若|MN|=
，则双曲线C的离心率 是（ ）
