题目内容
已知圆C的参数方程为
（
为参数），P是圆C与x轴的正半轴的交点.
（Ⅰ）求过点P的圆C的切线方程；
（Ⅱ）在圆C上求一点Q（a, b）,它到直线x+y+3=0的距离最长，并求出最长距离.
（为参数），P是圆C与x轴的正半轴的交点.（Ⅰ）求过点P的圆C的切线方程；
（Ⅱ）在圆C上求一点Q（a, b）,它到直线x+y+3=0的距离最长，并求出最长距离.
（1）x=2；（2）
，
.
，.（1）由P是圆C与x轴的正半轴的交点.得
，所以过点P的圆C的切线方程为x=2；
（2）法一：直接利用点到直线的距离公式求得
，由正弦函数的性质得，此时
.代入求得点Q的坐标.
解：（Ⅰ）过点P的圆C的切线为: x="2," -----------------------------------3分
（Ⅱ）法一：设
, -----------------------------------4分
则点Q（a, b）到直线x+y+3=0的距离为
当时,, -----------------------------------7分
这时
, 即 -----------------------------------8分
法二：用几何性质求得（略）
，所以过点P的圆C的切线方程为x=2；（2）法一：直接利用点到直线的距离公式求得
，由正弦函数的性质得，此时.代入求得点Q的坐标.解：（Ⅰ）过点P的圆C的切线为: x="2," -----------------------------------3分
（Ⅱ）法一：设
, -----------------------------------4分则点Q（a, b）到直线x+y+3=0的距离为
当
时,, -----------------------------------7分这时
, 即 -----------------------------------8分法二：用几何性质求得（略）
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
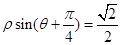，则极点到这条直线的距离是 . 
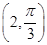到圆ρ＝2cosθ的圆心的距离为
中，以原点为极点，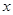
轴的正半轴为极轴建立极坐标系，设点A，B分别在曲线
：
（
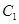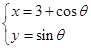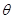为参数）和曲线
：
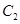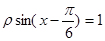上，则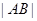
的最小值为 ． 
关于直线
对称的直线方程为 。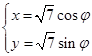
（
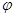为参数，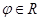
）上的点到曲线
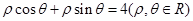的最短距离是
－
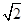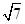
，半径为3的圆的极坐标方程.
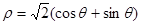的圆心坐标是（ ）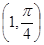
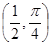
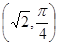
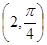
到直线
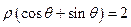的距离为