题目内容
已知数列{an}是等差数列,a4=15,S5=55,则过点P(4,a2010)和点Q(3,a2011)的直线的倾斜角是________.(用反三角函数表示结果)
π-arctan4
分析:由题意可得,a1+3d=15,5a1+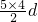 =55,解得 a1=3,d=4,直线的斜率为
=55,解得 a1=3,d=4,直线的斜率为  =-d=-4,由tanθ=-4,和θ 的范围,求出θ值.
=-d=-4,由tanθ=-4,和θ 的范围,求出θ值.
解答:设公差为d,由题意可得,a1+3d=15,5a1+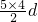 =55,解得 a1=3,d=4.
=55,解得 a1=3,d=4.
则过点P(4,a2010)和点Q(3,a2011)的直线的斜率为 =-d=-4,
=-d=-4,
设直线的倾斜角是θ,则 tanθ=-4,又 0≤θ<π,∴θ=π-arctan4,
故答案为π-arctan4.
点评:本题考查等差数列的定义和性质,通项公式,直线的倾斜角和斜率的关系,以及倾斜角的取值范围,已知三角函数值求角的大小,求出首项a1和公差d的值,是解题的关键.
分析:由题意可得,a1+3d=15,5a1+
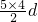 =55,解得 a1=3,d=4,直线的斜率为
=55,解得 a1=3,d=4,直线的斜率为  =-d=-4,由tanθ=-4,和θ 的范围,求出θ值.
=-d=-4,由tanθ=-4,和θ 的范围,求出θ值.解答:设公差为d,由题意可得,a1+3d=15,5a1+
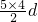 =55,解得 a1=3,d=4.
=55,解得 a1=3,d=4.则过点P(4,a2010)和点Q(3,a2011)的直线的斜率为
 =-d=-4,
=-d=-4,设直线的倾斜角是θ,则 tanθ=-4,又 0≤θ<π,∴θ=π-arctan4,
故答案为π-arctan4.
点评:本题考查等差数列的定义和性质,通项公式,直线的倾斜角和斜率的关系,以及倾斜角的取值范围,已知三角函数值求角的大小,求出首项a1和公差d的值,是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目