Question

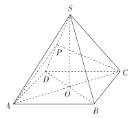
【题目】已知焦点在y轴上的椭圆E的中心是原点O，离心率等于，以椭圆E的长轴和短轴为对角线的四边形的周长为.直线与轴交于点P，与椭圆E相交于A，B两个点．

（I）求椭圆E的方程；

(II)若，求的取值范围．

Answer 1

【答案】(Ⅰ) ；（Ⅱ）(1，4).

【解析】试题分析：

(1)由题意求得a＝2，b＝1.∴椭圆E的方程为 ＋x2＝1.

(2)联立直线与椭圆的方程，结合判别式为正数得到关于m的不等式，求解不等式可得的取值范围是(1，4).

试题解析：

(I)根据已知设椭圆E的方程为＋＝1(a>b>0)，焦距为2c，

由已知得＝，∴c＝a，b2＝a2－c2＝.

∵以椭圆E的长轴和短轴为对角线的四边形的周长为4，

∴4＝2a＝4，∴a＝2，b＝1.∴椭圆E的方程为＋x2＝1.

(II)根据已知得P(0，m)，设A(x1，kx1＋m)，B(x2，kx2＋m)，

由得，(k2＋4)x2＋2mkx＋m2－4＝0.

由已知得Δ＝4m2k2－4(k2＋4)(m2－4)>0，即k2－m2＋4>0，且x1＋x2＝，x1x2＝.

由得x1＝－3x2.

∴3(x1＋x2)2＋4x1x2＝12x－12x＝0.

∴＋＝0，即m2k2＋m2－k2－4＝0.

当m2＝1时，m2k2＋m2－k2－4＝0不成立，∴k2＝.

∵k2－m2＋4>0，∴－m2＋4>0，即>0.∴1<m2<4.

∴m2的取值范围为(1，4)．