题目内容
设直线x=m分别交函数y=sinx、y=sin(x+| π | 2 |
分析:由已知中直线x=m分别交函数y=sinx、y=sin(x+
)的图象于M、N两点,构造函数表示M、N的距离,根据辅助角公式可将其化为一个正弦型函数的形式,根据正弦型函数的性质,即可得到答案.
| π |
| 2 |
解答:解:∵y=sin(x+
)=cosx
∵直线x=m分别交函数y=sinx、y=sin(x+
)的图象于M、N两点,
则|MN|=|sinx-cosx|
令f(x)=|sinx-cosx|=|
sin(x-
)|∈[0,
]
故M、N的距离的最大值为
故答案为:
| π |
| 2 |
∵直线x=m分别交函数y=sinx、y=sin(x+
| π |
| 2 |
则|MN|=|sinx-cosx|
令f(x)=|sinx-cosx|=|
| 2 |
| π |
| 4 |
| 2 |
故M、N的距离的最大值为
| 2 |
故答案为:
| 2 |
点评:本题考查的知识点是三角函数的最值,其中构造函数表示M、N的距离,将平面上两动点之间的距离问题转化为三角函数的最值问题,是解答本题的关键.

练习册系列答案
相关题目
 ,
, ,动直线x=t分别与函数y=f(x)、y=g(x)的图象分别交于点A(t,f(t))、B(t,g(t)),在点A处作函数y=f(x)的图象的切线,记为直线l1,在点B处作函数y=g(x)的图象的切线,记为直线l2.
,动直线x=t分别与函数y=f(x)、y=g(x)的图象分别交于点A(t,f(t))、B(t,g(t)),在点A处作函数y=f(x)的图象的切线,记为直线l1,在点B处作函数y=g(x)的图象的切线,记为直线l2.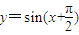 的图象于M、N两点,则M、N的距离的最大值为 .
的图象于M、N两点,则M、N的距离的最大值为 .