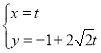题目内容
【题目】已知函数![]() ,无穷数列
,无穷数列![]() 的首项
的首项![]() .
.
(1)如果![]() ,写出数列
,写出数列![]() 的通项公式;
的通项公式;
(2)如果![]() (
(![]() 且
且![]() ),要使得数列
),要使得数列![]() 是等差数列,求首项
是等差数列,求首项![]() 的取值范围;
的取值范围;
(3)如果![]() (
(![]() 且
且![]() ),求出数列
),求出数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)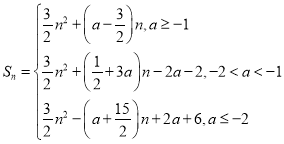 .
.
【解析】
(1)化简函数![]() 为分段函数,然后求出
为分段函数,然后求出![]() .
.
(2)由![]() 是等差数列,求出公差
是等差数列,求出公差![]() ,首项,然后求解
,首项,然后求解![]() 的范围.
的范围.
(3)当![]() 时,求出前
时,求出前![]() 项和,当
项和,当![]() 时,当
时,当![]() 时,分别求出
时,分别求出![]() 项和即可.
项和即可.
解:(1)![]() 函数
函数![]()
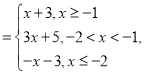
又![]() 且
且![]() ,
,![]() .
.
(2)因为![]() 是等差数列,则
是等差数列,则![]() ,
,![]() ,
,
由分段函数![]() 的解析式及等差数列的性质有
的解析式及等差数列的性质有![]() ,公差
,公差![]() .
.
当![]() 时,有
时,有![]() ,符合题意.
,符合题意.
当![]() 时,
时,![]() ,
,
由![]() 得
得![]() ,得
,得![]() ,
,![]() ,
,
又![]() ,则
,则![]() 无解.
无解.
当![]() 时,
时,![]() ,
,
由![]() 得
得![]() ,得
,得![]() ,此时
,此时![]() ,满足
,满足![]() .
.
综上所述,可得![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
(3)当![]() 时,
时,![]() ,
,
![]() 数列
数列![]() 是以
是以![]() 为首项,公差为
为首项,公差为![]() 的等差数列,
的等差数列,
![]()
![]() .
.
当![]() 时,
时,![]()
![]() ,
,
![]() 时,
时,![]() .
.
![]() 时,
时,![]() .
.
![]() 时,
时,![]()
![]()
![]()
又![]() 也满足上式,
也满足上式,![]()
![]()
当![]() 时,
时,![]()
![]() ,
,
![]() 时,
时,![]() .
.
![]() 时,
时,![]() .
.
![]() 时,
时,![]()
![]()
![]()
又![]() 也满足上式,
也满足上式,![]()
![]() .
.
综上所述: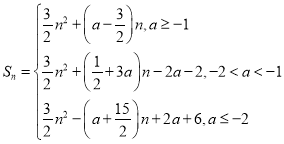 .
.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目