题目内容
已知a>0,函数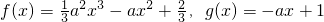
(Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求函数f(x)在(-1,1)上的极值;
(Ⅲ)若在区间 上至少存在一个实数x0,使f(x0)≥g(x0)成立,求实数a的取值范围.
上至少存在一个实数x0,使f(x0)≥g(x0)成立,求实数a的取值范围.
解:(Ⅰ)由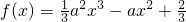 ,得:f′(x)=a2x2-2ax.
,得:f′(x)=a2x2-2ax.
当a=1时,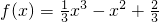 ,此时f′(1)=-1,
,此时f′(1)=-1,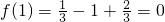 .
.
所以,f(x)在点(1,f(1))处的切线方程为y=-1×(x-1),即x+y-1=0;
(Ⅱ)由f′(x)=a2x2-2ax=0得:x=0,或x= ,
,
当0<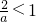 ,即a>2时,因为x∈(-1,1),
,即a>2时,因为x∈(-1,1),
由f′(x)>0?-1<x<0或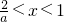 .
.
由f′(x)<0?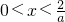 .
.
所以f(x)在(-1,0]上递增,在(0, ]上递减,在
]上递减,在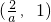 上递增.
上递增.
故在(-1,1)上,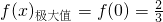 ,
,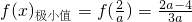 .
.
当 ,即0<a≤2时,f(x)在(-1,0)上单调递增,在(0,1)上递减
,即0<a≤2时,f(x)在(-1,0)上单调递增,在(0,1)上递减
故在(-1,1)上,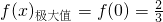 ,无极小值;
,无极小值;
(Ⅲ)设F(x)=f(x)-g(x)=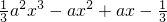 ,x∈[
,x∈[ ,
, ].
].
则F′(x)=a2x2-2ax+a=a2x2+a(1-2x).
因为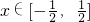 ,a>0,所以F′(x)>0.
,a>0,所以F′(x)>0.
故F(x)在区间 上为增函数.
上为增函数.
所以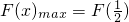 ,
,
若在区间 上至少存在一个实数x0,使f(x0)≥g(x0)成立,所以需F(x)max≥0.
上至少存在一个实数x0,使f(x0)≥g(x0)成立,所以需F(x)max≥0.
即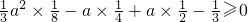 ,
,
所以a2+6a-8≥0.
解得: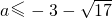 或
或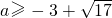 .
.
因为a>0,所以a的取值范围是[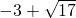 ,+∞).
,+∞).
分析:(Ⅰ)把a代入函数解析时候,求出f(1)及f′(1),利用直线方程的点斜式可求切线方程;
(Ⅱ)把原函数求导,得到导函数后求出导函数的零点,对a进行分类讨论得原函数在不同区间上的单调性,从而求出函数f(x)在(-1,1)上的极值;
(Ⅲ)利用函数的导函数求出函数f(x)与g(x)的差函数在 上的最大值,把在区间
上的最大值,把在区间 上至少存在一个实数x0,使f(x0)≥g(x0)成立,转化为两个函数f(x)与g(x)的差函数在
上至少存在一个实数x0,使f(x0)≥g(x0)成立,转化为两个函数f(x)与g(x)的差函数在 上的最大值大于等于0,然后列式可求a的范围.
上的最大值大于等于0,然后列式可求a的范围.
点评:本题考查了利用函数的导函数求曲线上点的切线方程的方法,考查了利用导函数求闭区间上的最值,考查了数学转化思想,解答此题的关键是把在区间 上至少存在一个实数x0,使f(x0)≥g(x0)成立,转化为两个函数f(x)与g(x)的差函数在
上至少存在一个实数x0,使f(x0)≥g(x0)成立,转化为两个函数f(x)与g(x)的差函数在 上的最大值大于等于0,该转化理解起来有一定难度.
上的最大值大于等于0,该转化理解起来有一定难度.
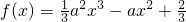 ,得:f′(x)=a2x2-2ax.
,得:f′(x)=a2x2-2ax.当a=1时,
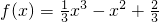 ,此时f′(1)=-1,
,此时f′(1)=-1,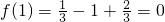 .
.所以,f(x)在点(1,f(1))处的切线方程为y=-1×(x-1),即x+y-1=0;
(Ⅱ)由f′(x)=a2x2-2ax=0得:x=0,或x=
 ,
,当0<
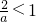 ,即a>2时,因为x∈(-1,1),
,即a>2时,因为x∈(-1,1),由f′(x)>0?-1<x<0或
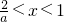 .
.由f′(x)<0?
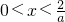 .
.所以f(x)在(-1,0]上递增,在(0,
 ]上递减,在
]上递减,在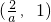 上递增.
上递增.故在(-1,1)上,
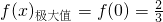 ,
,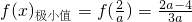 .
.当
 ,即0<a≤2时,f(x)在(-1,0)上单调递增,在(0,1)上递减
,即0<a≤2时,f(x)在(-1,0)上单调递增,在(0,1)上递减故在(-1,1)上,
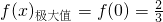 ,无极小值;
,无极小值;(Ⅲ)设F(x)=f(x)-g(x)=
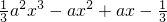 ,x∈[
,x∈[ ,
, ].
].则F′(x)=a2x2-2ax+a=a2x2+a(1-2x).
因为
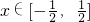 ,a>0,所以F′(x)>0.
,a>0,所以F′(x)>0.故F(x)在区间
 上为增函数.
上为增函数.所以
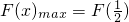 ,
,若在区间
 上至少存在一个实数x0,使f(x0)≥g(x0)成立,所以需F(x)max≥0.
上至少存在一个实数x0,使f(x0)≥g(x0)成立,所以需F(x)max≥0.即
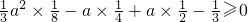 ,
,所以a2+6a-8≥0.
解得:
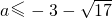 或
或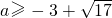 .
.因为a>0,所以a的取值范围是[
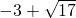 ,+∞).
,+∞).分析:(Ⅰ)把a代入函数解析时候,求出f(1)及f′(1),利用直线方程的点斜式可求切线方程;
(Ⅱ)把原函数求导,得到导函数后求出导函数的零点,对a进行分类讨论得原函数在不同区间上的单调性,从而求出函数f(x)在(-1,1)上的极值;
(Ⅲ)利用函数的导函数求出函数f(x)与g(x)的差函数在
 上的最大值,把在区间
上的最大值,把在区间 上至少存在一个实数x0,使f(x0)≥g(x0)成立,转化为两个函数f(x)与g(x)的差函数在
上至少存在一个实数x0,使f(x0)≥g(x0)成立,转化为两个函数f(x)与g(x)的差函数在 上的最大值大于等于0,然后列式可求a的范围.
上的最大值大于等于0,然后列式可求a的范围.点评:本题考查了利用函数的导函数求曲线上点的切线方程的方法,考查了利用导函数求闭区间上的最值,考查了数学转化思想,解答此题的关键是把在区间
 上至少存在一个实数x0,使f(x0)≥g(x0)成立,转化为两个函数f(x)与g(x)的差函数在
上至少存在一个实数x0,使f(x0)≥g(x0)成立,转化为两个函数f(x)与g(x)的差函数在 上的最大值大于等于0,该转化理解起来有一定难度.
上的最大值大于等于0,该转化理解起来有一定难度. 
练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
| A、?x∈R,f(x)≤f(x0) | B、?x∈R,f(x)≥f(x0) | C、?x∈R,f(x)≤f(x0) | D、?x∈R,f(x)≥f(x0) |
已知a>0,函数f(x)=(x2-2ax)ex的最小值所在区间是( )
A、(-∞,a-1-
| ||
B、(a-1-
| ||
| C、(0,2a) | ||
| D、(2a,+∞) |