Question

如图2-2-12所示,在半径为1的⊙O中,引两条互相垂直的直径AE和BF,在弧EF上取点C,弦AC交BF于P,弦CB交AE于Q.证明四边形APQB的面积是1.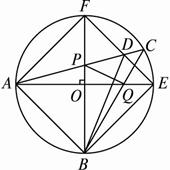

图2-2-12

Answer 1

思路分析:由已知条件可以证明四边形ABEF是正方形,且边长为,则正方形面积为2.而△ABD的面积为正方形面积的一半,所以,只需证明S_{四边形APQB} =S_△ABD,即证S_△BPD?=S_△BPQ?,即证DQ∥PB.因为BP⊥AE,所以,只需证DQ⊥AE.

证明:∵AE、BF为互相垂直的两条直径,垂足O为圆心,?

∴AE、BF互相平分、垂直且相等.∴四边形ABEF是正方形.?

∴∠ACB =∠AEF =45°,即∠DCQ =∠QED.?

∴D、Q、E、C四点共圆.连结CE、DQ,则∠DCE +∠DQE =180°.?

∵AE为⊙O的直径,∴∠DCE =90°,∠DQE =90°.?

∵∠FOE =90°,进而DQ∥BF,∴S_△BPQ =S_△BPD?,?

∴S_△ABP +S_△BPQ =S_△ABP +S_△BPD,即S_{四边形ABQP} =S_△ABD.?

∵⊙O的半径为1,∴正方形边长为,即AB =AF =.?

∴S_{四边形ABQP} =S_△ABD?= AB·AF =1.