题目内容
若至少存在一个 ,使得关于
,使得关于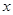 的不等式
的不等式 成立,则实数
成立,则实数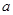 的取值范围为 .
的取值范围为 .

解析试题分析:问题转化为:至少存在一个 ,使得关于
,使得关于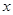 的不等式
的不等式 成立,令
成立,令 ,
, ,函数
,函数 与
与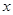 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,
,
(1)当函数 的左支与
的左支与 轴交于点
轴交于点 ,此时有
,此时有 ,若
,若 ,解得
,解得 或
或 ,
,
则当 时,在
时,在 轴右侧,函数
轴右侧,函数 的图象在函数
的图象在函数 的上方,不合乎题意;
的上方,不合乎题意;
(2)在 轴右侧,当函数
轴右侧,当函数 的左支与曲线
的左支与曲线 的图象相切时,函数
的图象相切时,函数 左支图象对应的解析式为
左支图象对应的解析式为 ,将
,将 代入
代入 得
得 ,即
,即 ,
,
令 ,即
,即 ,解得
,解得 ,则当
,则当 时,如下图所示,在
时,如下图所示,在 轴右侧,函数
轴右侧,函数 的图象在函数
的图象在函数 的上方或相切,则不等式
的上方或相切,则不等式 在
在 上恒成立,不合乎题意;
上恒成立,不合乎题意;
(3)当 时,如下图所示,在
时,如下图所示,在 轴右侧,函数
轴右侧,函数 的图象的左支或右支与函数
的图象的左支或右支与函数 相交,在
相交,在 轴右侧,函数
轴右侧,函数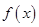 的图象中必有一部分图象在函数
的图象中必有一部分图象在函数 的下方,即存在
的下方,即存在 ,使得不等式
,使得不等式 成立,故实数
成立,故实数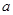 的取值范围是
的取值范围是 .
.
考点:不等式、函数的图象

练习册系列答案
相关题目
 的解集为
的解集为  使
使 成立,则实数
成立,则实数 的取值范围是
的取值范围是  ,满足
,满足 ,则
,则 ,
, 。
。 的解集是非空集合,则
的解集是非空集合,则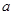 的取值范围是
的取值范围是  的解集是 ,
的解集是 , 的解集为空集,则实数
的解集为空集,则实数 的取值范围为
的取值范围为  的解集为___________.
的解集为___________.