Question

已知函数f（x）= ,g（x）=3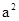lnx,其中a>0。若两曲线y=f（x）,y=g（x）有公共点，且在该点处的切线相同。则a的值为         。

Answer 1

解析试题分析：设公共点（x₀，y₀），根据题意得到，f（x₀）=g（x₀），f′（x₀）=g′（x₀），解方程组即可求出a的值．解：设y=f（x）与y=g（x）（x＞0）在公共点（x₀，y₀）处的切线相同
而f′（x）=x+2a，g′（x）= , 由题意可知f（x₀）=g（x₀），f′（x₀）=g′（x₀）， x₀²+2ax₀=3a²lnx₀,,那么解得x₀=a，a=,故答案为
考点：导数研究曲线上某点切线方程
点评：本题主要考查了利用导数研究曲线上某点切线方程、不等式的解法等基础知识，考查运算求解能力，属于中档题