题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c,已知 ,A=105°,C=5.
,A=105°,C=5.
(1)求角C的度数
(2)求b的长度.
 ,A=105°,C=5.
,A=105°,C=5.(1)求角C的度数
(2)求b的长度.
解:(1)∵(a+b+c)(a+b﹣c)=(2+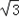 )ab,
)ab,
即a2+2ab+b2﹣c2=(2+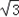 )ab,
)ab,
∴a2+b2﹣c2=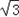 ab,
ab,
∴cosC=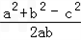 =
=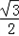 ,
,
C=30°
(2)∵A=105°,C=30°
∴B=45°.
由正弦定理得: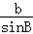 =
=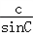 ,
,
∴b=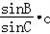 =
=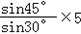 =5
=5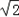 .
.
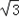 )ab,
)ab,即a2+2ab+b2﹣c2=(2+
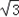 )ab,
)ab,∴a2+b2﹣c2=
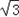 ab,
ab,∴cosC=
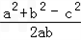 =
=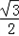 ,
,C=30°
(2)∵A=105°,C=30°
∴B=45°.
由正弦定理得:
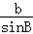 =
=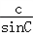 ,
,∴b=
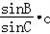 =
=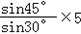 =5
=5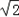 .
.
练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |