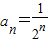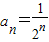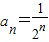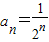题目内容
若{an}为递减数列，则{an}的通项公式可以为（ ）
| A、an=2n+3 | ||
| B、an=-n2+3n+1 | ||
C、an=
| ||
| D、an=（-1）n |
分析：要判定数列的单调性，根据单调性的定义，考虑利用an-an-1＜0进行检验即可．
解答：解：根据已知可得，an-an-1＜0
A：an=2n+3，an-an-1=2＞0，是递增的数列
B：an=-n2+3n+1，an-an-1=-2n-4，是先增后减
C：an=
，an-an-1=-
＜0是递减的数列
D：an=（-1）n是摆动数列，不具有单调性
故选C
A：an=2n+3，an-an-1=2＞0，是递增的数列
B：an=-n2+3n+1，an-an-1=-2n-4，是先增后减
C：an=
| 1 |
| 2n |
| 1 |
| 2n |
D：an=（-1）n是摆动数列，不具有单调性
故选C
点评：本题主要考查了利用数列单调性的定义判定数列的单调性，属于基本公式的应用，属于基础试题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
