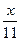题目内容
(本题12分)已知数列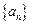 中,
中,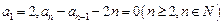 .
.
(1)写出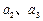 的值(只写结果),并求出数列
的值(只写结果),并求出数列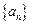 的通项公式;
的通项公式;
(2)设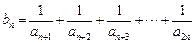 ,若对任意的正整数
,若对任意的正整数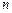 ,当
,当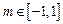 时,不等式
时,不等式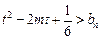 恒成立,求实数
恒成立,求实数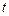 的取值范围。
的取值范围。
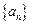 中,
中,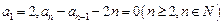 .
.(1)写出
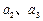 的值(只写结果),并求出数列
的值(只写结果),并求出数列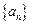 的通项公式;
的通项公式;(2)设
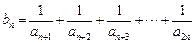 ,若对任意的正整数
,若对任意的正整数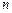 ,当
,当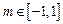 时,不等式
时,不等式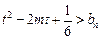 恒成立,求实数
恒成立,求实数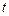 的取值范围。
的取值范围。(1)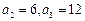 ,数列
,数列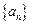 的通项公式为
的通项公式为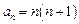
(2)实数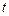 的取值范围为
的取值范围为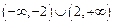
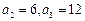 ,数列
,数列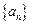 的通项公式为
的通项公式为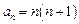
(2)实数
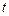 的取值范围为
的取值范围为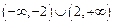
解:(1)∵ 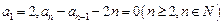 ∴
∴ 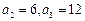 …………2分
…………2分
当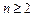 时,
时,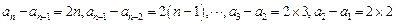 ,
,
∴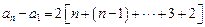 ,
,
∴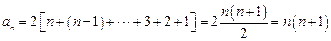 …………………3分
…………………3分
当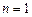 时,
时,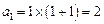 也满足上式, ∴数列
也满足上式, ∴数列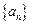 的通项公式为
的通项公式为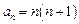 …1分
…1分
(2)
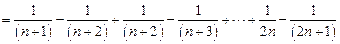
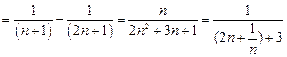 …………………2分
…………………2分
令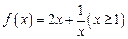 ,则
,则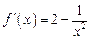 , 当
, 当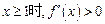 恒成立
恒成立
∴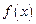 在
在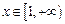 上是增函数,故当
上是增函数,故当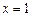 时,
时,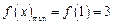
即当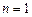 时,
时,  ……………2分
……………2分
要使对任意的正整数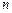 ,当
,当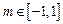 时,不等式
时,不等式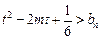 恒成立,则须使
恒成立,则须使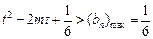 ,即
,即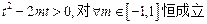 ,
,
∴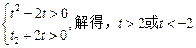 ∴ 实数
∴ 实数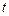 的取值范围为
的取值范围为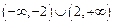 …2分
…2分
另解: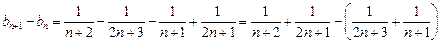 [
[
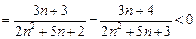 ∴ 数列
∴ 数列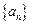 是单调递减数列,∴
是单调递减数列,∴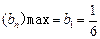
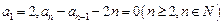 ∴
∴ 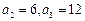 …………2分
…………2分当
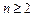 时,
时,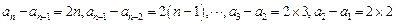 ,
,∴
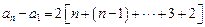 ,
,∴
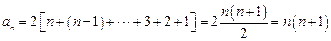 …………………3分
…………………3分当
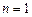 时,
时,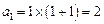 也满足上式, ∴数列
也满足上式, ∴数列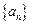 的通项公式为
的通项公式为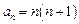 …1分
…1分(2)

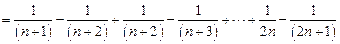
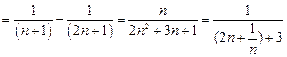 …………………2分
…………………2分令
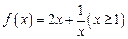 ,则
,则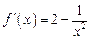 , 当
, 当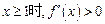 恒成立
恒成立∴
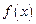 在
在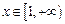 上是增函数,故当
上是增函数,故当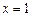 时,
时,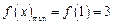
即当
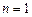 时,
时,  ……………2分
……………2分要使对任意的正整数
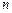 ,当
,当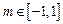 时,不等式
时,不等式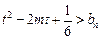 恒成立,则须使
恒成立,则须使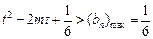 ,即
,即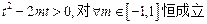 ,
,∴
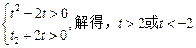 ∴ 实数
∴ 实数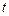 的取值范围为
的取值范围为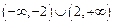 …2分
…2分另解:
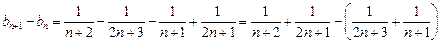 [
[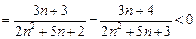 ∴ 数列
∴ 数列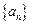 是单调递减数列,∴
是单调递减数列,∴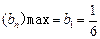

练习册系列答案
相关题目
 }中,
}中,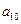 =18,前5项的和
=18,前5项的和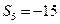
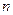 项和的最小值,并指出何时取最小.
项和的最小值,并指出何时取最小.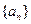 中,
中,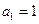 ,当
,当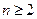 时,其前
时,其前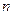 项和
项和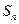 满足
满足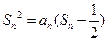 .
.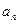 ;
;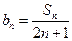 ,求数列
,求数列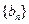 的前项和
的前项和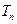 .
.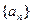 的前n项和为
的前n项和为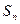 ,对一切正整数n,点
,对一切正整数n,点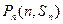 都在函数
都在函数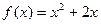 的图像上,且在点
的图像上,且在点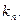
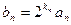 ,求数列
,求数列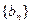 的前n项和
的前n项和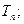
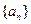 中,
中,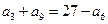 ,
, 表示数列
表示数列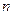 项和,则
项和,则 ( )
( )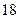


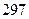
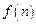 为
为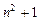
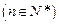 的各位数字之和,如:
的各位数字之和,如: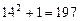 ,
,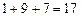 ,则
,则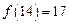 ;记
;记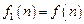 ,
,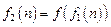 ,
,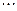 ,
,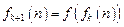 ,
,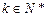 ,则
,则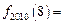 ( )
( )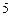
 和等比数列
和等比数列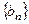 中,已知
中,已知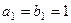 ,
, ,
, ;
; 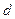 和
和 ;
;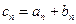 ,求数列
,求数列 的通项公式
的通项公式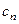 及前
及前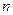 项和
项和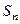 .
.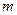 的三次幂可拆分成几个连续奇数的和,如右图所示,若
的三次幂可拆分成几个连续奇数的和,如右图所示,若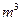 的“拆分数”中有一个数是2009,则
的“拆分数”中有一个数是2009,则
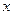 倍,则该工厂一年中的月平均增长率是( )
倍,则该工厂一年中的月平均增长率是( )