题目内容
设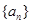 是公比大于1的等比数列,
是公比大于1的等比数列,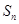 为数列
为数列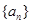 的前
的前 项和.已知
项和.已知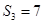 ,且
,且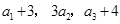 构成等差数列.
构成等差数列.
(1)求数列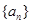 的通项公式;
的通项公式;
(2)令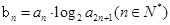 ,求数列
,求数列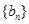 的前n项和
的前n项和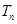 .
.
(1) (2)
(2)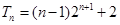
解析试题分析:(1)因为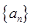 为等比数列,要求通项公式只要求出首项和公比,用
为等比数列,要求通项公式只要求出首项和公比,用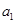 ,
, 表示
表示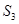 得出关系式,再根据
得出关系式,再根据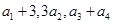 为等差数列,可解得答案。
为等差数列,可解得答案。
(2)由(1)得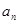 通项公式,带入可得
通项公式,带入可得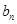 通项公式,为等差和等比乘积形式,再利用错位相减法可得前n相和
通项公式,为等差和等比乘积形式,再利用错位相减法可得前n相和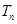 。
。
试题解析:(1)由已知得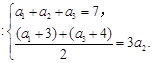 解得
解得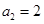 . 2分
. 2分
设数列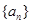 的公比为
的公比为 ,由
,由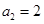 ,可得
,可得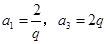 .
.
又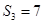 ,可知
,可知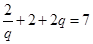 ,即
,即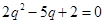 , 4分
, 4分
解得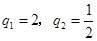 .由题意得
.由题意得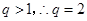 .
.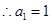 .
.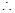
 6分
6分
(2)由(1)知,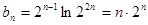 7分
7分
故 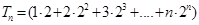
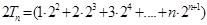 8分
8分
两式相减,可得: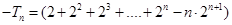 =
=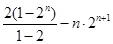 10分
10分
化简可得: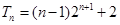 12分
12分
考点:等比数列性质,错位相减法。

练习册系列答案
相关题目
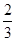 an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数. an
an 为等比数列,它的前n项和为Sn,a1=1,且
为等比数列,它的前n项和为Sn,a1=1,且 .
. 的通项公式;
的通项公式;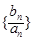 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列 的前n项和Tn.
的前n项和Tn.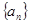 的公比为
的公比为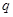 ,
,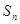 是
是 项和.
项和.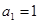 ,
,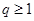 ,求
,求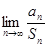 的值;
的值;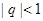 ,
,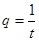 ,若首项
,若首项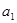 和
和 都是正整数,
都是正整数,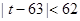 ,且对于任意正整数
,且对于任意正整数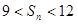 成立,问:这样的数列
成立,问:这样的数列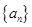 的前
的前 项和为
项和为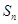 ,数列
,数列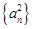 的前
的前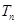 ,且
,且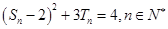 .
.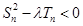 对
对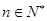 恒成立,求
恒成立,求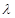 的最小值;
的最小值;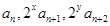 成等差数列,求正整数
成等差数列,求正整数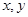 的值.
的值. ,设曲线
,设曲线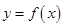 在点
在点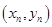 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数. 表示
表示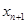 ;
;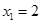 ,若
,若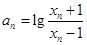 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前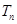 ,求
,求 中,
中,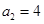 ;
;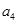 是
是 与
与 的等比中项.
的等比中项.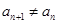 .求数列
.求数列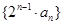 的前
的前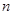 项和.
项和. 是各项都为正数的等比数列,
是各项都为正数的等比数列, 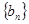 是等差数列,且
是等差数列,且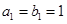 ,
,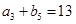 ,
,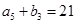 .
. 项和为
项和为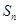 ,求数列
,求数列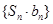 的前
的前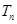 .
.