Question

已知函数f(x)=ax-x²的最大值不大于，又当x∈［,)时，f(x)≥.

(1)求a的值；

（2）设0＜a₁＜,a_n+1=f(a_n)，求证：0＜a_n＜.

Answer 1

思路解析：(1)由于f(x)=ax-x²的最大值不大于，所以f()=≤,即a²≤1.又x∈［,］时，f(x)≥.

所以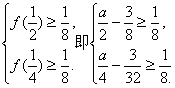解得a≥1.

∴a=1.

(2)①当n=1时，0＜a₁＜,不等式0＜a_n＜成立；

②假设n=k(k≥1)时，不等式成立，即0＜a_k＜,则当n=k+1时,

a_k+1=a_k(1-a_k)=·(k+2)a_k·(1-a_k)

因(k+2)a_k＞0,1-a_k＞0,

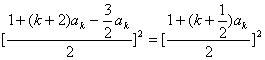∴(k+2)a_k·(1-a_k)≤＜1.

于是0＜a_k+1＜.

因此当n=k+1时，不等式成立.

综上所述由①②可知，对n∈N₊不等式0＜a_n＜成立.