题目内容
设椭圆C: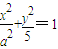 (a>0)的左右焦点分别为F1、F2,A是椭圆C上的一点,
(a>0)的左右焦点分别为F1、F2,A是椭圆C上的一点, ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为 |OF1|.
|OF1|.(Ⅰ)求椭圆C的方程;
(Ⅱ)设Q是椭圆C上的一点,过点Q的直线l交x轴于点F(-1,0),交y轴于点M,若|
 |=2|
|=2| |,求直线l的斜率.
|,求直线l的斜率.
【答案】分析:(Ⅰ)确定焦点坐标,求出A的坐标,可得AF1所在直线方程,求出坐标原点O到直线AF1的距离,利用坐标原点O到直线AF1的距离为 |OF1|,即可求椭圆C的方程;
|OF1|,即可求椭圆C的方程;
(Ⅱ)设出直线l的方程,利用|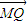 |=2|
|=2| |,确定Q的坐标,代入椭圆方程,即可求得结论.
|,确定Q的坐标,代入椭圆方程,即可求得结论.
解答:解:(Ⅰ)由题设知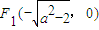 ,
, ,
,
由于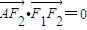 ,则有
,则有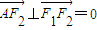 ,所以点A的坐标为
,所以点A的坐标为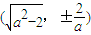 …(2分)
…(2分)
故AF1所在直线方程为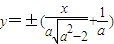 …(4分)
…(4分)
所以坐标原点O到直线AF1的距离为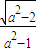
又|OF1|=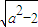 ,所以
,所以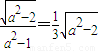 ,解得:a=2 …(6分)
,解得:a=2 …(6分)
∴所求椭圆的方程为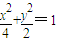 …(7分)
…(7分)
(Ⅱ)设直线l的方程为y=k(x+1),则有M(0,k) …(8分)
设Q(x1,y1),由于Q、F、M三点共线,且|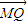 |=2|
|=2|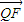 |,
|,
∴(x1,y1-k)=±2(x1+1,y1),解得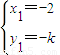 或
或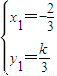 …(11分)
…(11分)
又Q在椭圆C上,故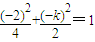 或
或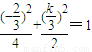 …(12分)
…(12分)
解得k=0或k=±4,所以所求直线l的斜率为0或±4 …(14分)
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查学生的计算能力,属于中档题.
 |OF1|,即可求椭圆C的方程;
|OF1|,即可求椭圆C的方程;(Ⅱ)设出直线l的方程,利用|
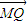 |=2|
|=2| |,确定Q的坐标,代入椭圆方程,即可求得结论.
|,确定Q的坐标,代入椭圆方程,即可求得结论.解答:解:(Ⅰ)由题设知
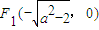 ,
, ,
,由于
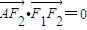 ,则有
,则有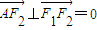 ,所以点A的坐标为
,所以点A的坐标为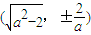 …(2分)
…(2分)故AF1所在直线方程为
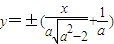 …(4分)
…(4分)所以坐标原点O到直线AF1的距离为
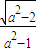
又|OF1|=
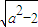 ,所以
,所以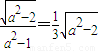 ,解得:a=2 …(6分)
,解得:a=2 …(6分)∴所求椭圆的方程为
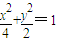 …(7分)
…(7分)(Ⅱ)设直线l的方程为y=k(x+1),则有M(0,k) …(8分)
设Q(x1,y1),由于Q、F、M三点共线,且|
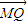 |=2|
|=2|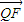 |,
|,∴(x1,y1-k)=±2(x1+1,y1),解得
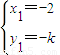 或
或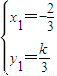 …(11分)
…(11分)又Q在椭圆C上,故
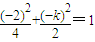 或
或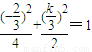 …(12分)
…(12分)解得k=0或k=±4,所以所求直线l的斜率为0或±4 …(14分)
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
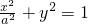 (a>0)的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C与圆x2+y2=c2有公共点.
(a>0)的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C与圆x2+y2=c2有公共点. ,求椭圆的方程;
,求椭圆的方程; (a>0)的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C与圆x2+y2=c2有公共点.
(a>0)的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C与圆x2+y2=c2有公共点. ,求椭圆的方程;
,求椭圆的方程; (a>0)的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C与圆x2+y2=c2有公共点.
(a>0)的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C与圆x2+y2=c2有公共点. ,求椭圆的方程;
,求椭圆的方程; (a>0)的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C与圆x2+y2=c2有公共点.
(a>0)的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C与圆x2+y2=c2有公共点. ,求椭圆的方程;
,求椭圆的方程;