题目内容
在数列{an}和{bn}中,bn是an和an+1的等差中项,a1=2且对任意n∈N*都有3an+1-an=0,则{bn}的通项bn=________.

分析:通过3an+1-an=0判断数列是等比数列,求出通项,然后利用bn是an和an+1的等差中项,求出bn.
解答:因为
 .
.∴{an}是公比为
 的等比数列
的等比数列
 .
.故答案为:
 .
.点评:本题是基础题,考查等比数列的判断通项公式的求法,等差中项的应用,考查计算能力.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
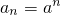 ,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.
,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.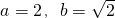 时,数列{bn}中的任意三项都不能构成等比数列.
时,数列{bn}中的任意三项都不能构成等比数列.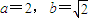 时,数列{bn}中的任意三项都不能构成等比数列;
时,数列{bn}中的任意三项都不能构成等比数列;