题目内容

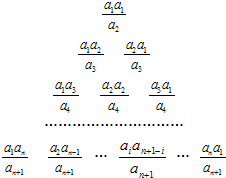精英家教网已知数列{an}满足：a1=1，a2=
1
2
，且an+2=
a2n+1
an+an+1
（n∈N*），则右图中第9行所有数的和为（　　）
A、90B、9!
C、1022D、1024
分析：由递推公式，得出a3，a4，a5，…，归纳出an =
1
n!
，据此得出第9行中各数的特点
aka10-k
a10
=Ck10．再各项求和．
解答：解：a1=1，a2=
1
2
，a3=
1
6
，a4=
1
24
，a5=
1
120
，…，an =
1
n!
．
aka10-k
a10
=
10!
k!(10-k)!
=C10k（k=1，2，3，…，9），
∴第9行所有数的和为C101+C102+C103+…+C109=1022
故选C
点评：数列的通项公式是研究数列的有力工具．本题中先探讨出数列{an}的通项公式，又得到了第9行所有数形成数列的通项公式．提纲挈领，妙趣横生．
练习册系列答案
相关题目
已知数列{an}满足：a1=1且an+1=
3+4an
12-4an
， n∈N*．
（1）若数列{bn}满足：bn=
1
an-
1
2
(n∈N*)，试证明数列bn-1是等比数列；
（2）求数列{anbn}的前n项和Sn；
（3）数列{an-bn}是否存在最大项，如果存在求出，若不存在说明理由．
已知数列{an}满足
1
2
a1+
1
22
a2+
1
23
a3+…+
1
2n
an=2n+1则{an}的通项公式
 
．
已知数列{an}满足：a1=
3
2
，且an=
3nan-1
2an-1+n-1
（n≥2，n∈N*）．
（1）求数列{an}的通项公式；
（2）证明：对于一切正整数n，不等式a1•a2•…an＜2•n！
已知数列{an}满足an+1=|an-1|（n∈N*）
（1）若a1=
54
，求an；
（2）若a1=a∈（k，k+1），（k∈N*），求{an}的前3k项的和S3k（用k，a表示）
（2012•北京模拟）已知数列{an}满足an+1=an+2，且a1=1，那么它的通项公式an等于
2n-1
2n-1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网