题目内容
如图所示,五面体A-BCC1B1中,AB1=4,底面△ABC是正三角形,AB=2,四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.
(1)若点D在线段AC上运动,试确定D的位置使AB1//平面BDC1,并说明理由;
 (2)当AB1//平面BDC1时,求二面角C-BC1-D的余弦值
(2)当AB1//平面BDC1时,求二面角C-BC1-D的余弦值
 解:(1)当D为AC的中点时,AB1//平面BDC1,证明如下:
解:(1)当D为AC的中点时,AB1//平面BDC1,证明如下:
连接B1C交BC1于O,连接DO,
∵四边形BCC1B1是矩形,∴O为B1C的中点,
又D为AC的中点,从而DO//AB1,∵AB1![]() 平面BDC1,DO
平面BDC1,DO![]() 平面BDC1,
平面BDC1,
∴AB1//平面BDC1.
(2)建立空间直角坐标系Bxyz,如图所示,则B(0,0,0),![]() ), ,
), , ![]()
![]()
![]()


练习册系列答案
相关题目
 如图所示的五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=
如图所示的五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=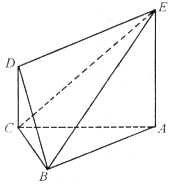 (II)在(I )的条件下,当k取得最大值时,求平面BDE与平面ABC所成角的大小.
(II)在(I )的条件下,当k取得最大值时,求平面BDE与平面ABC所成角的大小.
 (II)在(I )的条件下,当k取得最大值时,求平面BDE与平面ABC所成角的大小.
(II)在(I )的条件下,当k取得最大值时,求平面BDE与平面ABC所成角的大小.