题目内容
 如图,正四棱柱ABCD-A1B1C1D1的底面边长为
如图,正四棱柱ABCD-A1B1C1D1的底面边长为| 3 |
(Ⅰ)求证:A1C⊥平面AEF;
(Ⅱ)求二面角A-EF-B的大小;
(Ⅲ)求点B到平面AEF的距离.
分析:(Ⅰ)先利用AC1在平面A1B上的射影为A1B以及A1B⊥AE得到A1C⊥AE;同理A1C⊥AF即可证:A1C⊥平面AEF;
(Ⅱ)先由Rt△A1AB∽Rt△ABE,得到EB=1,AE=
=
;同理DF=1,AF=
;进而得DBEF是矩形,可知OG⊥EF,∠OGA是二面角A-EF-B的平面角,求出tan∠OGA即可;
(Ⅲ)利用VB1-AEF=VF-AEB1=VD-AEB1,得到h=
,通过求三角形的面积即可求出点B到平面AEF的距离.
(Ⅱ)先由Rt△A1AB∽Rt△ABE,得到EB=1,AE=
| 3-1 |
| 2 |
| 2 |
(Ⅲ)利用VB1-AEF=VF-AEB1=VD-AEB1,得到h=
| DA•S△AEB1 |
| S△AEF |
解答:解:(Ⅰ)∵CB⊥平面A1B,
∴AC1在平面A1B上的射影为A1B.
又A1B⊥AE,AE⊆平面A1B,
∴A1C⊥AE.
同理A1C⊥AF,
∴A1C⊥平面AEF.
(Ⅱ)∵A1B⊥AE,AA1⊥AB,
∴∠BA1A=∠EAB,
∴Rt△A1AB∽Rt△ABE,
∴
=
,EB=1,AE=
=
.
同理DF=1,AF=
.取EF和DB的中点G、O,连接AG、GO,
由AE=AF,得AG⊥EF,
由EB=FD,得DBEF是矩形,可知OG⊥EF.
∴∠OGA是二面角A-EF-B的平面角.
且tan∠OGA=
.
由AO=
,OG=1,
∴tanα=
.
∴α=arctan
.
即二面角A-EF-B的大小为arctan
.
(Ⅲ)设点B到平面AEF的距离是h.
由VB1-AEF=VF-AEB1=VD-AEB1,得
h•S△AEF=
DA•S△AEB1,
∴h=
.
由AG=
=
=
,EF=DB=
,
△AEF=
•EF•AG=
,
DA=
,S△AEB1=
×2×
=
,
∴h=
=
.
即点B到平面AEF的距离是
.
∴AC1在平面A1B上的射影为A1B.
又A1B⊥AE,AE⊆平面A1B,
∴A1C⊥AE.
同理A1C⊥AF,
∴A1C⊥平面AEF.
(Ⅱ)∵A1B⊥AE,AA1⊥AB,
∴∠BA1A=∠EAB,
∴Rt△A1AB∽Rt△ABE,
∴
| EB |
| AB |
| AB |
| A1A |
| 3-1 |
| 2 |
同理DF=1,AF=
| 2 |
由AE=AF,得AG⊥EF,
由EB=FD,得DBEF是矩形,可知OG⊥EF.
∴∠OGA是二面角A-EF-B的平面角.
且tan∠OGA=
| AO |
| OG |
由AO=
| ||
| 2 |
∴tanα=
| ||
| 2 |
∴α=arctan
| ||
| 2 |
即二面角A-EF-B的大小为arctan
| ||
| 2 |
(Ⅲ)设点B到平面AEF的距离是h.
由VB1-AEF=VF-AEB1=VD-AEB1,得
| 1 |
| 3 |
| 1 |
| 3 |
∴h=
| DA•S△AEB1 |
| S△AEF |
由AG=
| OG2+OA2 |
1+
|
| ||
| 2 |
| 6 |
△AEF=
| 1 |
| 2 |
| ||
| 2 |
DA=
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
∴h=
| 3 | ||||
|
2
| ||
| 5 |
即点B到平面AEF的距离是
2
| ||
| 5 |
点评:本题涉及到二面角的平面角及求法以及点到面的距离和线面垂直.一般在证明线面垂直时,通常转化为和平面内的两条相交直线垂直.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
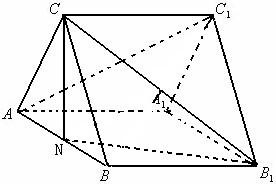 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
