题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且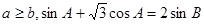 .
.
(1)求角C的大小;
(2)求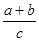 的最大值.
的最大值.
【答案】
(1)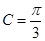 ;(2)2.
;(2)2.
【解析】
试题分析:本题考查两角和与差的正弦公式和三角函数最值以及解三角形中正弦定理的应用,考查运用三角公式进行三角变换的能力,考查运算能力.第一问,先利用两角和的正弦公式将等式的左边变形,再利用2个正弦值相等分析出2个角的关系,进行求角;第二问,先利用正弦定理,将边换成角,将第一问的结果代入,利用两角和的正弦公式化简表达式,最后利用三角函数值求最值.
试题解析:(1) ,即
,即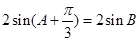 ,则
,则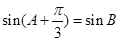 . 3分
. 3分
因为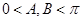 ,又
,又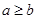 进而
进而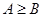 ,
,
所以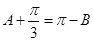 ,故
,故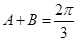 ,
,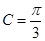 .
6分
.
6分
(2)由正弦定理及(1)得
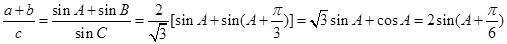 . 9分
. 9分
当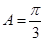 时,
时,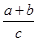 取最大值2. 10分
取最大值2. 10分
考点:1.两角和的正弦公式;2.正弦定理;3.三角函数最值.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |