题目内容
已知函数f(x)=ax-1(a>0且a≠1)(1)若函数y=f(x)的图象经过P(3,4)点,求a的值;
(2)比较
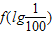 与f(-2.1)大小,并写出比较过程.
与f(-2.1)大小,并写出比较过程.
【答案】分析:(1)由函数y=f(x)的图象经过P(3,4),∴a2=4.又a>0,可得a的值.
(2)分a>1时和当0<a<1时两种情况,分别利用函数的单调性比较f(lg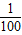 )与f(-2.1)的大小.
)与f(-2.1)的大小.
解答:解:(1)∵函数y=f(x)的图象经过P(3,4),∴a2=4.
又a>0,所以a=2.…(4分)
(2)当a>1时,f(lg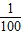 )>f(-2.1); 当0<a<1时,f(lg
)>f(-2.1); 当0<a<1时,f(lg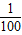 )>f(-2.1).
)>f(-2.1).
证明:由于f(lg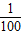 )=f(-2)=a-3;,f(-2.1)=a-3.1.
)=f(-2)=a-3;,f(-2.1)=a-3.1.
当a>1时,y=ax在(-∞,+∞)上为增函数,
∵-3>-3.1,∴a-3>a-3.1.即f(lg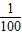 )>f(-2.1).…(8分)
)>f(-2.1).…(8分)
当0<a<1时,y=ax在(-∞,+∞)上为减函数,
∵-3>-3.1,∴a-3<a-3.1,故有f(lg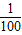 )<f(-2.1).…(12分)
)<f(-2.1).…(12分)
点评:本题主要考查指数函数的性质的综合应用,属于中档题.
(2)分a>1时和当0<a<1时两种情况,分别利用函数的单调性比较f(lg
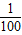 )与f(-2.1)的大小.
)与f(-2.1)的大小.解答:解:(1)∵函数y=f(x)的图象经过P(3,4),∴a2=4.
又a>0,所以a=2.…(4分)
(2)当a>1时,f(lg
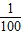 )>f(-2.1); 当0<a<1时,f(lg
)>f(-2.1); 当0<a<1时,f(lg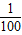 )>f(-2.1).
)>f(-2.1).证明:由于f(lg
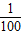 )=f(-2)=a-3;,f(-2.1)=a-3.1.
)=f(-2)=a-3;,f(-2.1)=a-3.1.当a>1时,y=ax在(-∞,+∞)上为增函数,
∵-3>-3.1,∴a-3>a-3.1.即f(lg
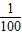 )>f(-2.1).…(8分)
)>f(-2.1).…(8分)当0<a<1时,y=ax在(-∞,+∞)上为减函数,
∵-3>-3.1,∴a-3<a-3.1,故有f(lg
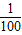 )<f(-2.1).…(12分)
)<f(-2.1).…(12分)点评:本题主要考查指数函数的性质的综合应用,属于中档题.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目