Question

直三棱柱ABC―A₁B₁C₁的侧棱长为3，底面边长A₁C₁=B₁C₁=1且∠A₁C₁B₁=90°，D点在棱AA₁上且AD=2DA₁，P点在棱CC₁上。

   （Ⅰ）求的最小值；

   （Ⅱ）在（Ⅰ）的条件下，求平面PDB₁与平面ABC所成的锐二面角的余弦植.

Answer 1

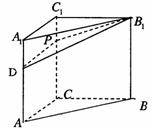
解：（Ⅰ）建立如图所示的直角坐标系，则D（1，0，2），B₁（0，1，3）

              

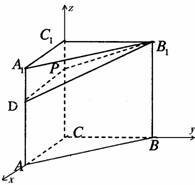
    设

∴

=   

所以，当取得最小值  

（Ⅱ）由（Ⅰ）知：

又

设平面PDB₁的法向量为，则

∴

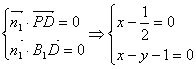
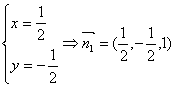
又平面ABC的法向量为   

∴

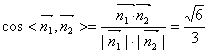
所以，平面PDB₁与平面ABC所成的锐二面角的余弦值为。