题目内容
设函数f(x)在定义域D上满足f( )=-1,f(x)≠0,且当x,y∈D时,f(x)+f(y)=f(
)=-1,f(x)≠0,且当x,y∈D时,f(x)+f(y)=f(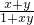 ).若数列{xn}中,
).若数列{xn}中,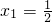 ,
,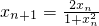 (xn∈D,n∈N×).则数列{f(xn)}的通项公式为
(xn∈D,n∈N×).则数列{f(xn)}的通项公式为
- A.f(xn)=2n-1
- B.f(xn)=-2n-1
- C.f(xn)=-3n+1
- D.f(xn)=3n
B
分析:由所给的函数关系式知 ,而数列之间又具备一个递推式,把递推式代入函数式得2f(xn)=f(xn+1),所以数列{f(xn)}是一个首项为-1,公比是2的等比数列,得到结果.
,而数列之间又具备一个递推式,把递推式代入函数式得2f(xn)=f(xn+1),所以数列{f(xn)}是一个首项为-1,公比是2的等比数列,得到结果.
解答:∵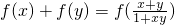 ,
,
∴ ,
,
∵ ,
,
∴2f(xn)=f(xn+1),
∴数列{f(xn)}是首项为-1,公比是2的等比数列,
∴f(xn)=-2n-1,
故选B
点评:数列可看作一个定义域是正整数集或它的有限子集的函数,当自变量从小到大依次取值对应的一列函数值,所以数列通常与函数知识结合起来,这种题目可以提高学生用函数的思想、方程的思想研究数列问题的自觉性、培养学生主动探索的精神和科学理性的思维方法.
分析:由所给的函数关系式知
 ,而数列之间又具备一个递推式,把递推式代入函数式得2f(xn)=f(xn+1),所以数列{f(xn)}是一个首项为-1,公比是2的等比数列,得到结果.
,而数列之间又具备一个递推式,把递推式代入函数式得2f(xn)=f(xn+1),所以数列{f(xn)}是一个首项为-1,公比是2的等比数列,得到结果.解答:∵
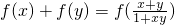 ,
,∴
 ,
,∵
 ,
,∴2f(xn)=f(xn+1),
∴数列{f(xn)}是首项为-1,公比是2的等比数列,
∴f(xn)=-2n-1,
故选B
点评:数列可看作一个定义域是正整数集或它的有限子集的函数,当自变量从小到大依次取值对应的一列函数值,所以数列通常与函数知识结合起来,这种题目可以提高学生用函数的思想、方程的思想研究数列问题的自觉性、培养学生主动探索的精神和科学理性的思维方法.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
设函数=f(x)在(-∞,+∞)内有定义,对于给定的正数K,定义函数fK(x)=
取函数f(x)=2-|x|.当K=
时,函数fK(x)的单调递增区间为( )
|
| 1 |
| 2 |
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,-1) |
| D、(1,+∞) |
设函数f(x)在(-∞,+∞)内有定义,对于给定的正数K,定义函数:fK(x)=
,取函数f(x)=a11(a>1).当K=
时,函数f(x)值域是( )
|
| 1 |
| a |
A、[0,
| ||
B、(0,
| ||
C、(0,1]∪[
| ||
D、(0,
|