题目内容
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() (点
(点![]() 在
在![]() 轴上方),斜率为
轴上方),斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,且
,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)设椭圆![]() 的离心率为
的离心率为![]() ,当点
,当点![]() 为椭圆
为椭圆![]() 的右顶点时,
的右顶点时,![]() 的坐标为
的坐标为 ,求
,求![]() 的值.
的值.
(2)若椭圆![]() 的方程为
的方程为![]() ,且
,且![]() ,是否存
,是否存![]() 在使得
在使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)![]() ,得
,得![]() 求解即可(2),
求解即可(2),![]() ,与椭圆联立消去y,由韦达定理得
,与椭圆联立消去y,由韦达定理得![]() 进而得
进而得![]() ,
,![]() ,由
,由![]() 得k的方程求解即可
得k的方程求解即可
(1)由题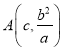 故
故 ![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
整理得![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
所以![]() .
.
(2)由(1)知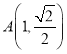 ,
,![]() ,即
,即![]() ,
,
联立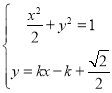 ,消去
,消去![]() ,得
,得![]() .
.
设点![]() 的横坐标为
的横坐标为![]() ,由韦达定理得
,由韦达定理得![]() ,即
,即![]() ,
,
所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
同理,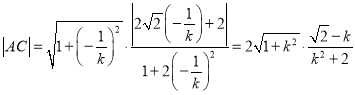 .
.
若有![]() ,则
,则![]() ,
,
即![]() ,而
,而![]() ,所以此方程无解,故不存在符合条件的k.
,所以此方程无解,故不存在符合条件的k.

练习册系列答案
相关题目
【题目】《最强大脑》是大型科学竞技类真人秀节目,是专注传播脑科学知识和脑力竞技的节目.某机构为了了解大学生喜欢《最强大脑》是否与性别有关,对某校的100名大学生进行了问卷调查,得到如下列联表:
喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
男生 | 15 | ||
女生 | 15 | ||
合计 |
已知在这100人中随机抽取1人抽到不喜欢《最强大脑》的大学生的概率为0.4
(I)请将上述列联表补充完整;判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关,并说明理由;
(II)已知在被调查的大学生中有5名是大一学生,其中3名喜欢《最强大脑》,现从这5名大一学生中随机抽取2人,抽到喜欢《最强大脑》的人数为X,求X的分布列及数学期望.
参考公式: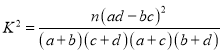 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.