Question

在正方体ABCD—A₁B₁C₁D₁中,P为DD₁的中点,O为底面ABCD的中心,求证:B₁O⊥平面PAC.

Answer 1

分析：欲证B₁O⊥平面PAC.只需证明与平面PAC内的两条相交直线都垂直,与它们的方向向量的数量积为0即可.

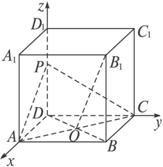
证明：如图，建立空间直角坐标系，不妨假设正方体的棱长为2，则A（2，0，0），P（0，0，1），C（0，2，0），B₁（2，2，2），O（1，1，0）.

于是=(1,1,2),=(-2,2,0),=(-2,0,1).由于·=-2+2=0，·=-2+2=0.

所以⊥AC,OB₁⊥AP.所以OB₁⊥平面PAC.

点拨：立体几何中的向量方法解决问题的“三步曲”：①建立立体图形与空间向量的联系，用空间向量表示问题中所涉及的点、线、面,把立体几何问题转化为向量问题;②通过向量运算,研究点,直线,平面之间的关系;③根据运算结果的几何意义来解释相关问题.