题目内容
一个递增的等差数列{an}，前三项的和a1+a2+a3=12，且a2，a3，a4+1成等比数列，则数列{an}的公差为（ ）
| A．±2 | B．3 | C．2 | D．1 |
∵a2，a3，a4+1成等比数列，
∴a32=a2•（a4+1），
∵数列{an}为递增的等差数列，设公差为d，
∴（a1+2d）2=（a1+d）（a1+3d+1），即a1+d=d2，
又数列{an}前三项的和a1+a2+a3=12，
∴a1+（a1+d）+（a1+2d）=12，即a1+d=4，
∴d2=4，即d=2或d=-2（舍去），
则公差d=2．
故选C
∴a32=a2•（a4+1），
∵数列{an}为递增的等差数列，设公差为d，
∴（a1+2d）2=（a1+d）（a1+3d+1），即a1+d=d2，
又数列{an}前三项的和a1+a2+a3=12，
∴a1+（a1+d）+（a1+2d）=12，即a1+d=4，
∴d2=4，即d=2或d=-2（舍去），
则公差d=2．
故选C
练习册系列答案
相关题目
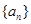，前三项的和
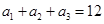，且
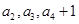成等比
数列，则数列
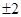B．3
C．2
D．1