题目内容
已知函数![]()
(1) 当![]() 时,求函数
时,求函数![]() 的最值;
的最值;
(2) 求函数![]() 的单调区间;
的单调区间;
(3) 试说明是否存在实数![]() 使
使![]() 的图象与
的图象与![]() 无公共点.
无公共点.
解:(1) 函数f(x)=x2-ax-aln(x-1)(a∈R)的定义域是(1,+∞)
当a=1时,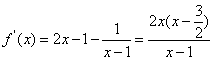 ,所以f (x)在
,所以f (x)在![]() 为减函
为减函
在![]() 为增函数,所以函数f (x)的最小值为
为增函数,所以函数f (x)的最小值为![]() =
=![]() .
.
(2) 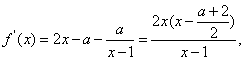
若a≤0时,则![]() f(x)
f(x)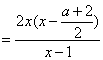
![]() 在(1,+∞)恒成立,所以f(x)的增区间为(1,+∞).
在(1,+∞)恒成立,所以f(x)的增区间为(1,+∞).
若a>0,则![]() 故当
故当![]() ,
, ![]()
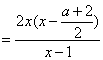
![]() ,
,
当![]() 时,f(x)
时,f(x) 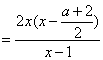
![]() ,
,
所以a>0时f(x)的减区间为![]() ,f(x)的增区间为
,f(x)的增区间为![]() .
.
(3) a≥1时,由(1)知f(x)在(1,+∞)的最小值为![]() ,
,
令![]()
![]() 在 [1,+∞)上单调递减,
在 [1,+∞)上单调递减,
所以![]() 则
则![]() >0,
>0,
因此存在实数a(a≥1)使f(x)的最小值大于![]() ,
,
故存在实数a(a≥1)使y=f(x)的图象与![]() 无公共点.
无公共点.

练习册系列答案
相关题目
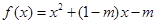
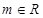 ,解不等式
,解不等式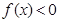 ;
;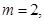 解不等式
解不等式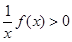

 时,求
时,求 上的最大值、最小值:
上的最大值、最小值: 的单调区间;
的单调区间;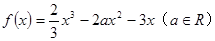
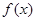 在(-1,1)内是减函数,求
在(-1,1)内是减函数,求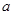 的取值范围
的取值范围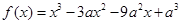 .
.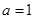 ,求函数
,求函数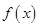 的极值;
的极值;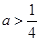 ,且当
,且当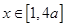 时,
时,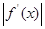
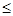 12a恒成立,试确定
12a恒成立,试确定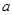 的取值范围.
的取值范围.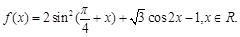
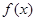 的最小正周期和单调增区间;
的最小正周期和单调增区间;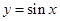 的图像经过怎样的变换得到?(写出变换过程)
的图像经过怎样的变换得到?(写出变换过程) 中,若
中,若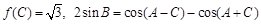 ,求
,求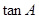 的值 .
的值 .